"האי"
בשנת 2007 עלתה לאוויר בערוץ הילדים סדרת הדרמה והמדע-בדיוני לילדים "האי". עלילת הסדרה עוקבת אחר חבורת נערים ישראלים הנשלחת אל אי בודד בבוקר בו אסטרואיד פוגע בכדור הארץ ומשמיד את כלל האנושות.
כאשר "האי" שודרה לראשונה בשנת 2007 הייתי בערך בן 10. הסדרה הייתה מאוד פופולארית וכמו כל שאר חבריי לכיתה, כמובן שצפיתי בה.
בתחילת הסדרה אנחנו לומדים כי לדמות הראשית יש ספר ציורים אדום. הספר הוא פריט עלילתי מהותי, וכבר בפרקים הראשונים של הסדרה הוא נגנב – לא ברור על ידי מי. כמה פרקים לאחר מכן מוצאים הנערים על האי מצלמת פולרואיד שיכולה לצלם את העבר. כמובן שהנערים מיד מבינים כי בעזרת המצלמה הם יכולים לגלות מה קרה לספר ומי גנב אותו. הבעיה היחידה היא, שהם לא יודעים מהו התאריך והשעה המדויקים בהם נלקח הספר, לאורך שנה שלמה שהם נמצאים על האי.
הנערים מנסים לכוון את המצלמה אל רגעים אקראיים במהלך השנה החולפת ולצלם תמונות רבות, אך תוך זמן קצר מבינים את חוסר היעילות של שיטת הפעולה הזו: ראשית, השיטה מבולגנת וגם אם יעבדו מסודר וכרונולוגית, ייקח להם זמן רב מדי למצוא את התאריך הנכון. שנית, הם לא יודעים מה מגבלת התמונות שהמצלמה מאפשרת להם לצלם ולכן עדיף לפתור את הבעיה תוך צילום כמות תמונות מינימלית. בנוסף, לא ידוע לכמה חלקים כדאי לחלק את השנה כדי להגיע לרמת דיוק מספקת. האם מספיק למצוא את השעה הנכונה, או את הדקה, או את השנייה?
מהר מאוד הם מוצאים את הפתרון לבעיה:
הפתרון המוצע הוא לחלק את השנה לשני חצאים על ידי צילום תמונה ביום אמצע השנה. אם הספר לא מופיע בתמונה, הוא נגנב כבר ולכן היעלמותו התרחשה בחצי השנה הראשונה. לעומת זאת, במידה והספר מופיע בתמונה, הרי שהוא עדיין לא נגנב והיעלמותו קרתה במהלך חצי השנה השני. בדיוק באותו האופן ניתן לחלק את חצי השנה הרלוונטי לשני רבעים, ואת רבע השנה הרלוונטי לשתי שמיניות, וכהנה וכהנה עד אשר יגיעו אל היום בו נעלם הספר, אשר אותו ניתן לחלק לשני מקטעים של 12 שעות, ומשם ל6 שעות, 3 שעות, שעה וחצי, 45 דקות וכהנה וכהנה כאשר במידת הצורך ניתן לדייק עד רמת השנייה.
לצורך השוואה, באמצעות השיטה הזו ניתן למצוא את תאריך היעלמות הספר על ידי צילום של עד 9 תמונות במקרה הרע ביותר, ואת השנייה המדויקת של היעלמות הספר על ידי צילום של עד 25 תמונות עבור המקרה הרע ביותר. לעומת זו, בשיטה המקורית אותה ניסו הנערים מציאת התאריך לבדו עשויה לקחת עד 365 תמונות (כמספר הימים בשנה) ואילו עבור מציאת השנייה המדויקת ידרשו לצלם כמות אדירה של עד 31,536,000 תמונות (כמספר השניות בשנה)
מיונים לצה"ל
כאשר הייתי בכיתה י"א, זומנתי על ידי צה"ל לסדרת מיונים עבור תפקידי מחשוב שונים. באחד מימי המיון בחנו את יכולות המועמדים בתכנות ופתירת בעיות אלגוריתמיות. אחת המשימות שקיבלתי הייתה לכתוב קוד אשר מוצא מהו השורש הריבועי של מספר נתון, ללא שימוש בפעולות השורש והחזקה. מיד התחלתי במלאכה, כאשר האלגוריתם הסופי שלי נראה ככה:
- המספר שעבורו אנו רוצים למצוא שורש הוא n
- נגדיר x שווה ל-0
- נחזור על תתי-השלבים הבאים כל עוד x כפול x לא שווה ל-n:
- נגדיל את x ב-1
- השורש של n הוא x
ואז בדקתי את עצמי: נניח שאני רוצה למצוא את השורש של 9. נגדיר x שווה לאפס. אפס כפול אפס שווה לאפס, ואפס לא שווה 9. לכן נגדיל את אפס באחת. אחת כפול אחת שווה אחת, ואחת לא שווה 9. לכן נגדיל את אחת באחת. שתיים כפול שתיים שווה ארבע, וארבע לא שווה 9. לכן נגדיל את שתיים באחת. שלוש כפול שלוש שווה 9, ולכן נמשיך הלאה לשלב הבא. השורש של 9 הוא x כאשר x שווה 3. זהו הפתרון הנכון והקוד עובד!
הראיתי את הקוד שלי לאחראי עליי. הוא אמר שהקוד עובד, אבל אך ורק עבור מספרים בעלי שורש ריבועי שלם או מספרים קטנים יחסית. חשבתי על מה שהוא אמר והבנתי את הבעיות:
עבור n = 5 לדוגמה, הקוד שלי לא יעצור אף פעם וימשיך לרוץ לנצח, כי השורש של 5 הוא 2.236 והאלגוריתם שלי מדלג עליו ועובר לנסות את 3 אחרי שהוא מנסה את 2. גם אם הייתי מקטין את הקפיצה בין בדיקה לבדיקה מ-1 למספר עשרוני קטן יותר, לכל שורש של n שונה, מספר שונה של ספרות לאחר הנקודה העשרונית. הגדרת "קפיצה" קטנה מאוד אינה יעילה עבור ערכי n קטנים או בעלי שורשים שלמים. לדוגמה, אין טעם לקפוץ ב-0.001 עבור n = 9 כי השורש שלו הוא 3.
בעיה נוספת היא שהאלגוריתם שלי לא יעיל עבור ערכי n גדולים. לדוגמה, עבור n = 1,000,000 האלגוריתם שלי יחזיר תשובה, אבל עד שזה יקרה הוא יצטרך לחזור על שלב 3.1 במשך אלף פעמים, וזה יותר מדי.
חשבתי שוב ושוב על הבעיות בקוד שלי: יותר מדי חזרות, רמת הדיוק הנחוצה לא ידועה לי. פתאום קפץ לי לראש זיכרון ישן, כזה שהדהים אותי שבכלל זכרתי. כשהדמויות ב"האי" רצו למצוא את הספר הם עמדו בדיוק בפני אותן שתי בעיות. כמה נוח! אני אעשה בדיוק מה שהם עשו. הפתרון שלהם יפתור גם את הבעיות שלי. ניגשתי לכתוב את האלגוריתם שלי מחדש וכעת הוא נראה כך:
- המספר שעבורו אנו רוצים למצוא שורש הוא n
- נגדיר גבול תחתון = 0
- נגדיר גבול עליון = n
- נגדיר אמצע = גבול עליון פחות גבול תחתון, לחלק ל-2
- נגדיר רמת דיוק = חמש ספרות לאחר הנקודה
- כל עוד מספר הספרות לאחר הנקודה של (n פחות (אמצע כפול אמצע)) גדול מרמת הדיוק:
- אם אמצע כפול אמצע גדול מ-n:
- נגדיר מחדש את גבול עליון עם הערך של אמצע
- נגדיר מחדש את אמצע עם הערך של גבול תחתון ועוד ((הערך הנוכחי של אמצע פחות גבול תחתון)חלקי 2)
- אחרת:
- נגדיר מחדש את גבול תחתון עם הערך של אמצע
- נגדיר מחדש את אמצע עם הערך של גבול עליון פחות ((גבול עליון פחות הערך הנוכחי של אמצע)חלקי 2)
- אם אמצע כפול אמצע גדול מ-n:
- נעגל את אמצע לפי רמת דיוק
- השורש של n הוא אמצע
האלגוריתם החדש קצת מורכב יותר לקריאה, אך בפשטות עושה בדיוק מה שהדמויות עשו בסדרה. ראשית קובעים רמת דיוק, כדי לקבוע בכמה ספרות לאחר הנקודה העשרונית אנו מסתפקים. אחר כך האלגוריתם מוצא את המספר האמצעי בין אפס למספר אשר רוצים למצוא את השורש שלו, ובודק אם ריבוע האמצע פחות המספר המקורי קטן יותר מרמת הדיוק. כל עוד הדיוק לא מספק, האלגוריתם יבדוק האם תוצאת ריבוע האמצע גדולה או קטנה מהמספר המבוקש ויחצה את טווח הפתרונות האפשריים שוב ושוב. כאשר האלגוריתם מוצא פתרון (אמצע של מקטע) שעומד ברמת הדיוק שקבענו מראש, האלגוריתם יעגל את הפתרון לפי רמת הדיוק ויסיים לרוץ. עיגול התשובה הסופית נחוץ, כי בלעדיו פתרונות שלמים עלולים להתקבל עם סטיות מיותרות, לדוגמה עבור n = 16 תתקבל התוצאה 4.0000067 לפני העיגול, ולאחריו הפתרון הסופי יהיה 4.
הראיתי לבוחן האחראי עליי את האלגוריתם החדש. כעת הוא נראה מרוצה, הודיע לי שזה הכל להיום ושיודיעו לי אם עברתי אל שלב המיון הבא, אליו זימנו אותי בערך חודש לאחר מכן. תודה לך, "האי".
האוניברסיטה
מאז אותו היום חלפו לא מעט שנים, והיום אני כבר סטודנט באוניברסיטה. בסמסטר הנוכחי אחד מהקורסים שאני לומד נקרא "מבוא למדעי המחשב", זהו קורס שנועד לבסס רקע בתחום מדעי המחשב.
השבוע הנוכחי הוא שבוע 5 של הסמסטר ובקורס התחלנו ללמוד על יעילות של אלגוריתמים ועל סיבוכיות זמן ריצה, כלומר, כיצד אלגוריתמים שונים יכולים לפתור את אותה הבעיה תוך פרקי-זמן שונים וכמויות חישובים שונות. אלגוריתם יעיל הוא כזה שידרוש כמות מינימלית של חישובים ובכך זמן השלמתו יהיה מינימלי.
על מנת להדגים את הנושא, המרצה הציג בפנינו אלגוריתמי חיפוש שונים, כלומר, אלגוריתמים שמטרתם בהינתן מבנה נתונים נתון היא למצוא בתוכו אובייקט העונה על הגדרות רצויות. אחד האלגוריתמים שהמרצה הציג, אשר קרוי "חיפוש בינארי", משך מיד את תשומת ליבי:
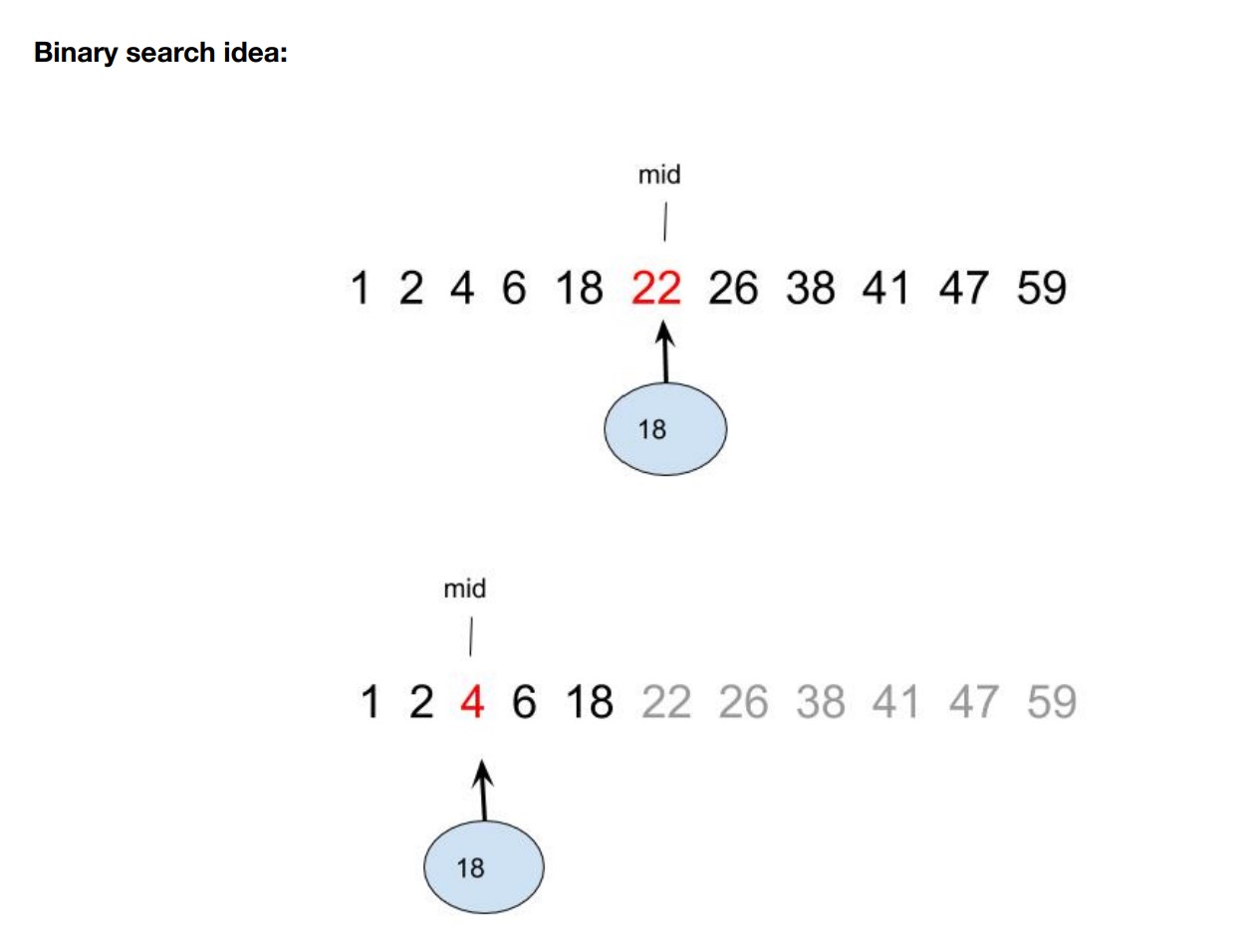
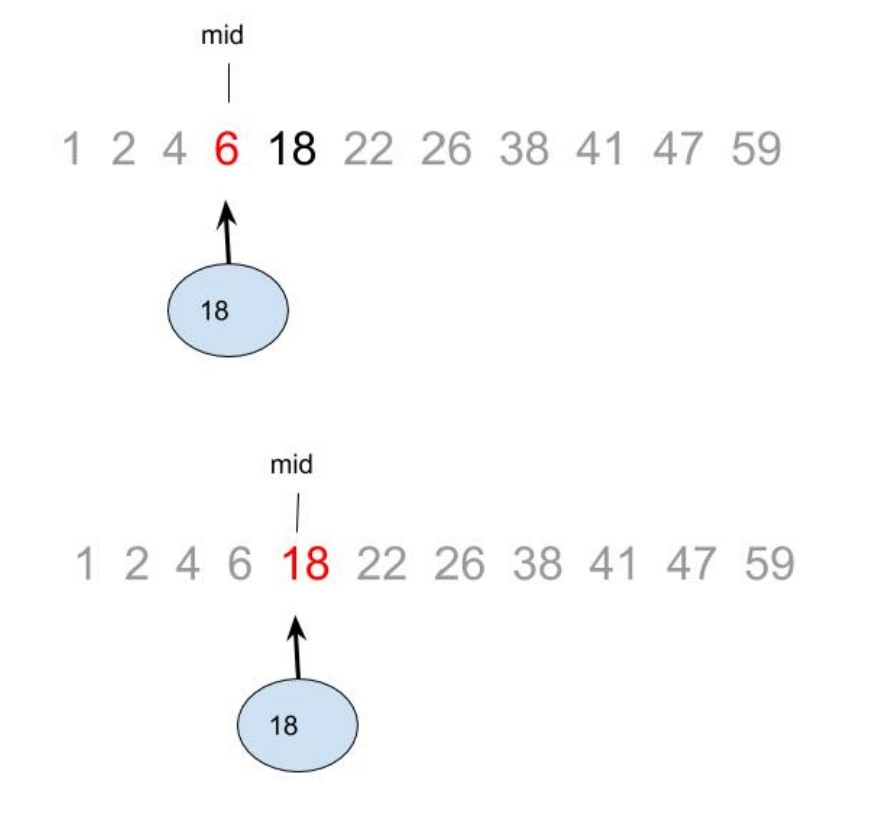
לא סתם האלגוריתם הזה מוכר לי! הוא כמובן אותו האלגוריתם בו הילדים השתמשו כדי למצוא את הספר, ובהשראתם אני השתמשתי בו כדי לעבור את המיונים בכיתה י"א! ועכשיו מלמדים אותי אותו בקורס באוניברסיטה. מצחיק.
האלגוריתם נקרא חיפוש בינארי בעקבות החלוקה החוזרת של מקטע החיפוש לשתי קבוצות שוות בגודלן. אלגוריתם התואם את הטקטיקה הראשונית של הנערים בסדרה "האי" למציאת הספר נקרא "חיפוש לינארי", וגם הוא הוצג באותה ההרצאה באוניברסיטה.
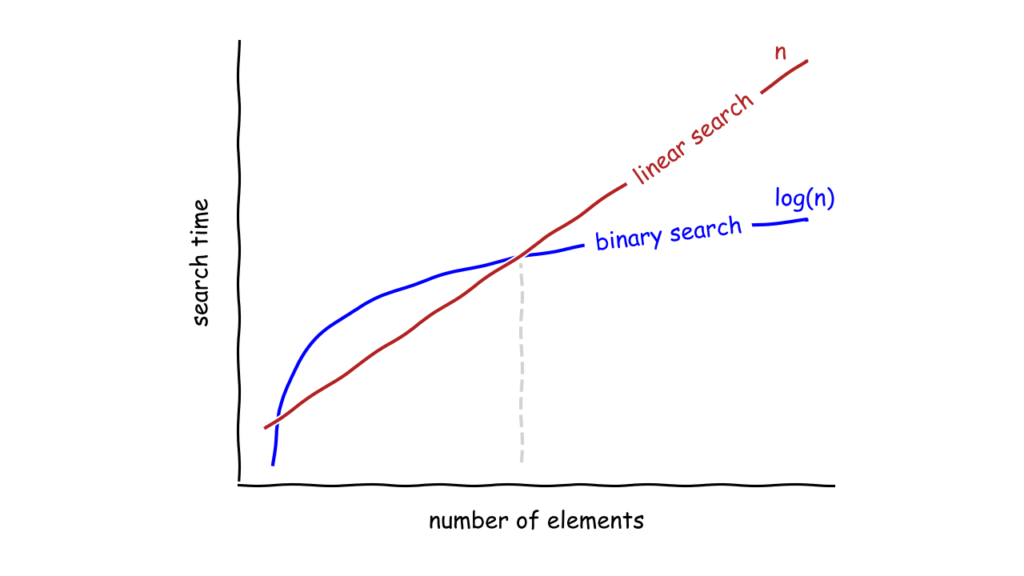
אמנם בדקנו את ההבדלים בין האלגוריתמים ספציפית עבור בעיית השורש, אך למעשה המסקנות שהסקנו רלוונטיות גם כמעט עבור כל משימה אחרת:
| קריטריון | חיפוש בינארי | חיפוש לינארי |
|---|---|---|
| יעיל במשאבים עבור מספרים גדולים | ✓ | X |
| יעיל במשאבים עבור מספרים קטנים | ✓ | ✓ |
| שימושי עבור רמת דיוק משתנה | ✓ | X |
| שימושי עבור רמת דיוק ידועה | ✓ | ✓ |
| עוזר למצוא את הספר האדום | ✓ | X |
לסיכום, המסקנה העיקרית שלי מהסיפור הזה היא שאפשר ללמוד דברים "מועילים" מכל אחד ומכל מקום, אפילו במקומות לא צפויים. אני סקרן האם לתסריטאים שכתבו את "האי" יש רקע במדעי המחשב או שזה צירוף מקרים.
כמה הערות לסיום:
- סיבוכיות זמן הריצה של חיפוש לינארי הינה O(n) וסיבוכיות של חיפוש בינארי הינה O(log(n)).
- למעשה קיימים אלגוריתמים לחישוב שורשים ריבועיים אשר יעילים בהרבה מאשר חיפוש בינארי. רוב המחשבונים שלנו, הן הפיזיים והן הדיגיטליים, מחשבים שורשים באמצעות שלל קירובים ושיטות שונות כגון טורי טיילור כאשר כל אחד מהם מתאים למקרים מסוימים.
- האנושות מתעסקת בלפענח דרכים לחישוב שורשים ריבועיים החל מהמאה ה-17 לפני הספירה ועד היום.


וואלק מעניין ביותר