בפוסטים הקודמים בסדרה הכרנו את הבסיס הפיזיקלי העומד מאחורי חשמל, והתחלנו לקרות מעגלים חשמליים פשוטים. כעת נוכל לנתח ולהרכיב מעגלים חשמליים מעט מורכבים יותר.

מעגלים חשמליים מגיעים בכל מיני צורות רבות ומשונות:

בהינתן מעגלים חשמליים שכאלו, נרצה שיהיו לנו הכלים לנתח אותם – כלומר לקבוע מה יהיו הזרם והמתח החשמליים בכל נקודה ונקודה. כדי שנוכל לעשות זאת נגדיר שתי דרכים בהן רכיבים חשמליים עשויים להיות מחוברים זה לזה:

חיבור בטור ובמקביל

כאשר רכיבים מחוברים זה לזה כך שכניסתו של רכיב אחד מחוברת אך ורק ליציאתו של הרכיב הקודם, נאמר שהרכיבים מחוברים בטור.

חיבור טורי של שתי נורות

מנגד, כאשר רכיבים מחוברים כך שכניסותיהם מחוברות זו לזו, ויציאותיהם מחוברות גם הן, נאמר שהרכיבים מחוברים במקביל ושכל אחד מהם נמצא בענף נפרד של המעגל. לנקודת חיבור הענפים נקרא "צומת".

חיבור מקבילי של שתי נורות

את התנהגות המתח והזרם במעגלים חשמליים מרובי רכיבים אנו מתארים באמצעות צמד חוקי קירכהוף (Kirchhoff's Laws):

חוקי קירכהוף

חוק המתחים של קירכהוף

חוק המתחים של קירכהוף (Kirchhoff's voltage law) קובע כי סכום המתחים הנופלים על רכיבים המחוברים בטור זה לזה, שווה למתח על הענף כולו.

החוק תקף למספר רכיבים גדול כרצוננו. עבור n רכיבים מתקיים:

V_{total}=V_{1}+V_{2}+V_{3}+…V_{n}=\sum \limits_{n=1}^{k}V_{n}

חוק הזרמים של קירכהוף

חוק הזרמים של קירכהוף (Kirchhoff's Current Law) קובע כי סכום הזרמים הנכנסים לצומת שווה לסכום הזרמים היוצאים ממנה, וכי דרך ענף יחיד הזרם נשאר קבוע בכל נקודה:

בשרטוט לעיל ניתן לראות n ענפים הנושאים n זרמים שונים, נכנסים אל תוך צומת. מן הצומת יוצא ענף יחיד הנושא את הזרם I_{total}.

I_{1}+I_{2}+I_{3}+…=I_{total}

או בכתיב מקוצר:

\sum \limits_{i=1}^{n}I_{n}=I_{total}

דוגמאות

דוגמה 1

נניח מעגל שבו מתח עבודה שגודלו Vdd מחובר בטור לשני נגדים שהתנגדותיהם R_{1}, R_{2}:

נסמן את הזרם בענף כ-I, לכן לפי חוק אוהם המתח שנופל על נגד R_{1} הוא

(1)   \begin{equation*} V_{1}=R_{1} \cdot I\end{equation*}

והמתח שנופל על נגד R_{2} הוא

(2)   \begin{equation*} V_{2}=R_{2} \cdot I\end{equation*}

המתח על כל הענף הוא V_{DD} ומכך, לפי חוק המתחים של קירכהוף נובע כי

V_{DD}=V_{1}+V_{2}=R_{1} \cdot I+R_{2} \cdot I

או בהצגה מפושטת:

V_{DD}=I\cdot (R_{1}+R_{2})

כלומר:

(3)   \begin{equation*} I=\frac{V_{DD}}{(R_{1}+R_{2})}\end{equation*}

נציב את משוואה (3) ב-(1) וב- (2) ונקבל:

V_{1}=V_{DD}\frac{R_{1}}{(R_{1}+R_{2})}

V_{2}=V_{DD}\frac{R_{2}}{(R_{1}+R_{2})}

כלומר הגענו למסקנה כי עבור נגדים המחוברים בטור, המתח הנופל על כל נגד הוא מכפלת החלק היחסי של התנגדות הנגד מתוך התנגדות כלל הענף, במתח על כל הענף. רעיון זה נקרא "מחלק מתחים". מקרה פרטי של זה הוא עבור נגדים בעלי התנגדות שווה, אשר מתח הענף יתחלק ביניהם באופן שווה כל שעל כך נגד ייפול מתח זהה.

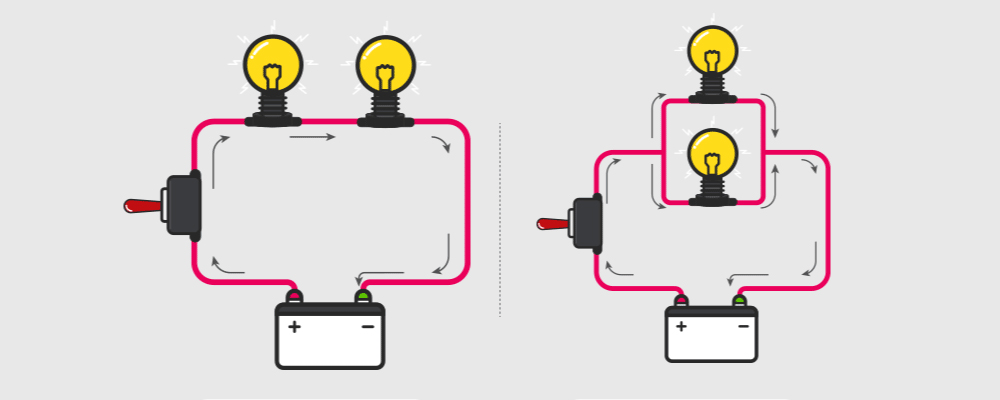
לחיבור זה שני חסרונות. ראשית, המתח מתחלק בין הרכיבים. לדוגמה, שתי נורות המחוברות זו לזו בטור יאירו בעוצמה נמוכה יותר מזו שמתח העבודה של המעגל מאפשר אם היו מחוברות במקביל. כמו כן, החסרון השני הוא שבמידה ואחת הנורות נשרפת, היא הופכת לנתק והזרם במעגל ייפסק. מכך, גם הנורה השנייה תפסיק להאיר.

דוגמה 2

נניח מעגל שבו מתח עבודה שגודלו Vdd מחובר במקביל לשני נגדים שהתנגדותיהן R_{1}, R_{2}:

נסמן את הזרם בענף הראשי של המעגל כ-i. על שני הנגדים נופל אותו מתח, לכן לפי חוק אוהם הזרם שעובר דרך נגד R_{1} הוא

(4)   \begin{equation*} I_{1}=\frac{V_{DD}}{R_{1}}\end{equation*}

והזרם שעובר דרך נגד R_{2} הוא

(5)   \begin{equation*} I_{2}=\frac{V_{DD}}{R_{2}}\end{equation*}

ומכך, לפי חוק הזרמים של קירכהוף נובע כי

i=I_{1}+I_{2}=\frac{V_{DD}}{R_{1}}+\frac{V_{DD}}{R_{2}}

או בהצגה מפושטת:

i=V_{DD}\cdot \frac{R_{1}+R_{2}}{R_{1}\cdot R_{2}}

כלומר:

(6)   \begin{equation*} V_{DD}=i\cdot \frac{R_{1}\cdot R_{2}}{R_{1}+R_{2}}\end{equation*}

נציב את משוואה (6) ב-(4) וב- (5) ונקבל:

I_{1}=i\cdot \frac{R_{2}}{(R_{1}+R_{2})}

I_{2}=i\cdot \frac{R_{1}}{(R_{1}+R_{2})}

כלומר הגענו למסקנה כי עבור שני נגדים המחוברים במקביל, הזרם הזורם דרך כל נגד הוא מכפלת החלק היחסי של התנגדות הנגד האחר מתוך התנגדות כלל הענף, בזרם הנכנס לענף. רעיון זה נקרא "מחלק זרמים". מקרה פרטי של זה הוא עבור נגדים בעלי התנגדות שווה, אשר הזרם יתחלק ביניהם באופן שווה.

בניגוד לדוגמה הקודמת, במעגל זה המתח הנופל על הרכיבים זהה. לדוגמה, נורות המחוברות זו לזו במקביל יאירו שתיהן בעוצמה המקסימלית שמתח העבודה מאפשר. בנוסף, במידה ואחת הנורות נשרפת, השנייה תמשיך לעבוד ולהאיר.

מודולאריות

אחד הדברים השימושיים שחוקי קירכהוף מאפשרים לנו לעשות זה לקבץ רכיבים.

קיבוץ נגדים בטור

נחזור לדוגמת שני הנגדים המחוברים בטור, אך הפעם נצייר סביבם קופסה דימיונית:

ננסה לחשוב על הקופסה שלנו כעל רכיב שלם. היא מורכבת מנגדים בלבד, ולכן היא מתנהגת כמו נגד. נסמן את ההתנגדות שלה בתור R_{box}. נרצה לחשב מה הערך של R_{box}, ולשם כך אנחנו יכולים להשתמש בחוק אוהם:

R_{box}=\frac{V_{DD}}{I}

לפי חוק הזרמים של קירכהוף הזרם נשאר קבוע לאורך הענף, וכבר ראינו במשוואה (3) מה ערכו של אותו הזרם. נוכל להציב אותו בנוסחה של R_{box} ונקבל:

R_{box} = \cancel{V_{DD}}\cdot\frac{(R_{1}+R_{2})}{\cancel{V_{DD}}}=R_{1}+R_{2}

כלומר שני הנגדים שחיברנו בטור שקולים לנגד יחיד. ערכו של נגד זה שווה לסכום התנגדויות שני הנגדים המקוריים.

באותו האופן ניתן לקבץ כל מספר נגדים המחוברים בטור לכדי נגד אחד שקול, כאשר התנגדותו תהיה שווה לסכום ערכי הנגדים

R_{total}=R_{1}+R_{2}+...+R_{k}=\sum \limits_{n=1}^{k}R_{n}

קיבוץ נגדים במקביל

גם נגדים המחוברים במקביל ניתנים לקיבוץ. נחזור לדוגמה 2 ונצייר קופסה מסביב לשני הנגדים.

גם הפעם מתקיים

R_{box}=\frac{V_{DD}}{I}

נציב במתח את ערכו שמצאנו קודם לכן במשוואה (6) ונקבל:

R_{box}=\frac{R_{1}\cdot R_{2}}{R_{1}+R_{2}}=(\frac{1}{R_{1}}+\frac{1}{R_{2}})^{-1}

במקרים רבים מקובל לסמן חיבור של נגדים במקביל על ידי האופרטור || לדוגמה:

R_{box}=(\frac{1}{R_{1}}+\frac{1}{R_{2}})^{-1}=R_{1}||R_{2}

באותו האופן נוכל לחבר במקביל כל מספר של נגדים, והם יהיו שקולים לנגד יחיד שהתנגדותו:

R_{total}=(\frac{1}{R_{1}}+\frac{1}{R_{2}}+...+\frac{1}{R_{k}})^{-1}=(\sum \limits_{n=1}^{k}\frac{1}{R_{n}})^{-1}

סיכום

כל הכלים שלמדנו עד כה מספיקים כדי לאפשר לנו לנתח את המתחים והזרמים במעגלים חשמליים באופן תיאורטי וחישובי. בפוסט הבא בסדרה נראה כיצד מודדים את התכונות של המעגלים חשמליים באופן מעשי.