שער לוגי הוא ייצוג של פונקציה לוגית בוליאנית (מילים מפונפנות ל"פעולה") הפועלת על קלטים, ומוציאה פלטים בהתאם.
השערים הלוגיים פועלים על שני ערכים בלבד: "אמת" ו"שקר" (או לחילופין, 0 או 1). את פעולת השערים הלוגיים ניתן לתאר על ידי "טבלת אמת" בה מתוארים הפלטים עבור כל קומבינציה של הקלטים, או לחלופין על ידי אלגברה בוליאנית – צמצום של האלגברה המוכרת לנו לכדי שימוש בשני סימנים בלבד, 0 ו-1.
ההסבר הזה יכול להישמע די מבלבל, לכן עדיף פשוט להתחיל להסתכל על דוגמאות.
חוצץ
השער הכי בסיסי הוא שער buffer (חוצץ), אשר לו כניסה יחידה ומוצא (פלט) יחיד.
את שער זה משרטטים בתור משולש, כאשר הכניסה מתחברת אל בסיסו והיציאה מחוברת אל הקודקוד.
המוצא של שער זה תמיד יהיה זהה לכניסתו, כלומר אם הכניסה היא 0 המוצא יהיה 0, ואם הכניסה היא 1 המוצא יהיה 1. ניתן לסכם את הקשר בין הכניסה והיציאה בטבלה הבאה, אשר נקראת "טבלת אמת":
| out | in |
|---|---|
| 0 | 0 |
| 1 | 1 |
באלגרה בוליאנית נתאר את השער על ידי הביטוי הפשוט
מחשבה מתבקשת היא, מה בכלל התועלת של רכיב כזה טריויאלי. הרי לא עשינו שום פעולה על הכניסה, יכולנו פשוט לקצר בין in ל-out. בעוד חוצצים הם באמת חסרי תועלת מבחינה לוגית, מבחינה חשמלית יש להם יתרונות רבים בתוך מעגל: חציצה בין הזרמים בכניסה ובמוצא, הוספת דיליי לתזמוני המעגל, קישור בין חלקי מעגל עם קיבולים שונים, ועוד.
אלו נושאים מעט מתקדמים יותר בתכנון מעגלים ולכן בינתיים נחשוב על החוצץ בתור שער טריויאלי בלבד.
מהפך
שער בסיסי נוסף הוא שער NOT (מהפך), אשר לו כניסה יחידה ומוצא יחיד.
המוצא של שער זה תמיד יהיה ההפך של כניסתו, כלומר אם הכניסה היא 0 המוצא יהיה 1, ואם הכניסה היא 1 המוצא יהיה 0. העיגול שבקצה שרטוט השער מסמל היפוך – ואכן שער זה הוא ההיפוך של שער החוצץ.
| out | in |
|---|---|
| 1 | 0 |
| 0 | 1 |
באלגרה בוליאנית נתאר את השער על ידי הביטוי
הקו מעל in מסמן היפוך של הערך שמוחזק בו, כלומר 0 יהפוך ל-1 ו-1 יהפוך ל-0.
גם
שער בסיסי נוסף הוא שער AND (וגם), אשר לו שתי כניסות ומוצא אחד
המוצא של שער זה יהיה 1 רק כאשר שתי הכניסות שלו יהיו 1, כלומר אם הכניסה A היא 1 וגם הכניסה B היא 1, המוצא יהיה 1. עבור כל מקרה אחר המוצא יהיה 0.
| out | B | A |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
באלגברה בוליאנית נתאר את השער על ידי הביטוי
הרעיון בנוטציה זו, הוא שעבור כפל הביטוי מתאפס אם לפחות אחד מגורמי המכפלה הוא אפס. אם אף אחד מהם לא 0, האפשרות היחידה שנותרה היא ששניהם 1, והמכפלה תהיה 1.
או
עוד שער נפוץ הוא שער OR (או), אשר לו שתי כניסות ומוצא אחד
על מנת שהמוצא של שער זה יהיה 1 מספיק שאחת הכניסות תהיה 1. כלומר, המוצא יהיה 0 אך ורק כאשר גם הכניסה A וגם הכניסה B יהיו 0. עבור כל מקרה אחר המוצא יהיה 1.
| out | B | A |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
באלגברה בוליאנית נתאר את השער על ידי הביטוי
הרעיון בנוטציה זו, הוא שבעת חיבור, הביטוי מתאפס אך ורק אם שני גורמי החיבור הם אפס. עבור 1 ו-0 הסכום יהיה 1, ועבור 1 ו-1 הסכום יהיה 2, אך כיוון שאנחנו עוסקים באלגברה בוליאנית אין מספר 2, ולכן הסכום יהיה 1.
נאנד
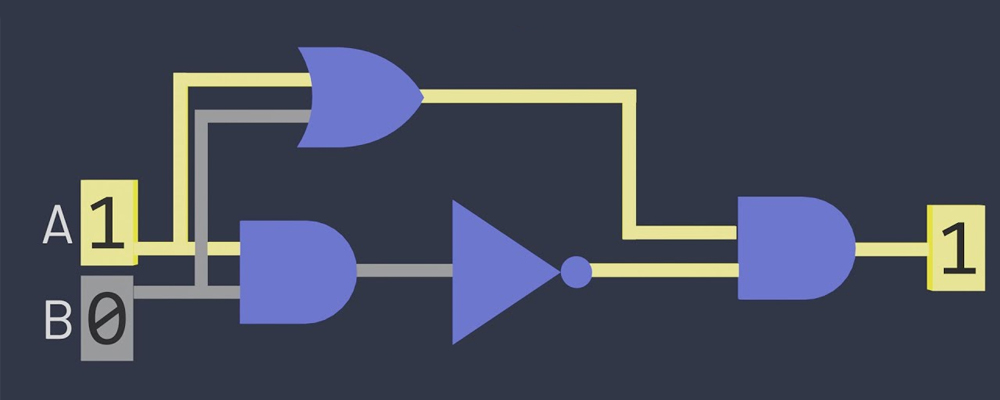
אפשר גם לשרשר שערים אחד אחרי השני, למשל:
הביטוי באלגברה בוליאנית עבור שרשור השערים יהיה:
כלומר לוקחים את המוצא של שער AND ומהפכים אותו. שרשור זה נפוץ מאוד, ולכן הוא נחשב לשער לוגי בפני עצמו: שער NAND, קיצור של NOT AND. השרטוט המפושט שלו נראה כמו שער AND עם טבעת על המוצא, המסמנת היפוך.
טבלת האמת של שער נאנד תראה כך:
| out | B | A |
|---|---|---|
| 1 | 0 | 0 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
נור
בדיוק באותו האופן נוכל לשרשר שער OR אל שער NOT:
הפעם הביטוי באלגברה בוליאנית עבור שרשור השערים יהיה:
גם שרשור זה נפוץ מאוד ולכן קיבל שם ושרטוט מפושט משל עצמו: שער NOR, קיצור של NOT OR. השרטוט המפושט שלו יראה כמו שער OR שהוסיפו ביציאתו טבעת, שגם פה מסמלת היפוך.
טבלת האמת של שער נור תראה כך:
| out | B | A |
|---|---|---|
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
קסור
השער האחרון בו נדון ברשומה זו הוא שער XOR – קיצור של Exclusive Or. הביטוי של שער זה באלגברה בוליאנית יהיה:
כלומר, הפלט יהיה 1 אך ורק עבור ערכי A,B השונים זה מזה. שער זה דומה מעט לשער OR, אך אינו מקבל את המצב בו שני הקלטים הם 1.
טבלת האמת של XOR נראית כך:
| out | B | A |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |

כתיבת תגובה