הקובייה האלקטרונית של אפיק

הקדמה
מבוא למעגלים חשמליים
מבוא לאלקטרוניקה דיגיטלית
הקובייה האלקטרונית
1. מבוא לקובייה אלקטרונית
2. הרכיבים בקובייה
  1. מהפך שמיט טריגר CD4584
  2. מונה בינארי CD4518
אופן הפעולה של הקובייה
סיכום

בכיתה ג' הייתי בחוג אלקטרוניקה

של חברת "אפיק אלקטרוניקה". אני זוכר שזה היה חוג די מגניב בסך הכל:

פעם בשבוע קבוצה של 10-20 ילדים נפגשת עם מדריך למשך שעה וחצי של חשיפה והיכרות עם עולם האלקטרוניקה. לומדים איך זורם חשמל ומה זה מעגל חשמלי, פוגשים רכיבים חשמליים שונים כמו נגד ולד ודיודה, וכמובן שיש גם את החלק המעשי – עובדים עם מלחמים ובדיל ובמהלך השנה כל ילד מרכיב בעצמו מספר מעגלים חשמליים.

באמת שאחלה חוג.

אז למה אני בכלל טורח לכתוב על זה?

היום כשכבר יש לי כלים להבין איתם את תחום האלקטרוניקה, אני מבין שרוב הזמן לא באמת למדתי אלקטרוניקה בחוג הזה. וזה לא באמת אשמת החוג, לא לגמרי. כי אמנם החלק התיאורטי של החוג היה זעיר לעומת החלק המעשי, ואמנם ברובו המוחלט של הזמן הלחמנו רכיבים ללוח בלי להבין מה התפקיד שלהם שם או איך הם גורמים למעגל להתנהג כמו שהוא אמור – אבל להצליח להעביר את המידע הזה בשלמותו לילד בן 8 זה ממש לא בא ברגל. אפילו להסביר אותו לאדם מבוגר זאת משימה לא פשוטה בכלל.

כפי שאני מקווה שתיווכחו בהמשך רשומה זו, הדרך להבנה אמיתית ומלאה של מעגלים אלקטרוניים שכאלו עוברת דרך הבנת כמות אדירה של מושגים ורעיונות עמוקים במתמטיקה, לוגיקה ופיזיקה.

חשבתי שיהיה מעניין לבחור אחד מהפרויקטים שבניתי בחוג אלקטרוניקה בכיתה ג' – בדיוק את אותו מעגל חשמלי – לנסות להבין את אופן הפעולה שלו בעצמי ואחר כך להנגיש את הניתוח שלו כמה שניתן, לכל מי שרק מעוניין להבין. מ-א' עד ת', עם כמה שפחות נפנופי ידיים וכמה שפחות קיצורי דרך, בשפה פשוטה ככל האפשר.

מבוא למעגלים חשמליים

לפני שאנחנו בכלל מתחילים, חובה להבין רעיונות מפתח בחשמל כגון מטען חשמלי, מתח חשמלי וזרם חשמלי. על מושגים אלו הרחבתי בעבר ברשומה הזו.

אחרי שביססנו את המושגים הללו, יש להכיר רכיבים חשמליים בסיסיים כמו מקור מתח, נגד, קבל ודיודה. בנוסף יש להכיר את חוק אוהם – $V=I\cdot R$ – המקשר בין מתחים וזרמים ברכיבים התנגדותיים. על כך ועוד אפשר לקרוא בפוסט הזה.

לבסוף, יש להכיר את ההבדל בין חיבור בטור וחיבור במקביל, וכיצד לנתח מעגלים חשמליים באמצעות חוקי קירכהוף. בנוסף מומלץ לדעת לקבץ נגדים וקבלים לרכיבים שקולים. על כל אלה ניתן לקרוא כאן.

מבוא לאלקטרוניקה דיגיטלית

בחוג האלקטרוניקה של אפיק כל הפרויקטים היו ממומשים באלקטרוניקה דיגיטלית.

מה זה אומר בכלל אלקטרוניקה דיגיטלית?

באלקטרוניקה דיגיטלית אנחנו מגדירים שתי רמות מתח – מתח גבוה ומתח נמוך. באמצעות רמות המתח האלה אנחנו יכולים לייצג מידע בבסיס בינארי, כאשר מתח ברמה הנמוכה ייצג את הספרה 0 ומתח ברמה הגבוהה ייצג את הספרה 1.

על כל מקטע במעגל שבו המתח מתאים לרמת המתח הגבוהה, נגיד שהוא "שווה 1 לוגית". על על כל מקטע במעגל בו המתח מתאים לרמת המתח הנמוכה, נגיד שהוא "שווה 0 לוגית".

בדרך כלל נרצה לבחור את רמת המתח הגבוהה להיות מתח העבודה של המעגל (מתח מקור המתח), ואת רמת המתח הנמוכה להיות $0V$ . לדוגמה, בחוג של אפיק כל הפרויקטים מופעלים על ידי סוללת 9V. לכן רמות המתח שלהם מוגדרות כך שרמת המתח הגבוהה היא 9V ורמת המתח הנמוכה היא 0V.

בסיס בינארי

כיוון שבאלקטרוניקה דיגיטלית אנחנו עובדים עם שתי רמות מתח בלבד – 0 ו-1 – נוכל לייצג מידע (=מספרים) רק באמצעות שני סימנים אלו. הדרך לייצג כל מספר באמצעות שני סימנים היא שימוש בבסיס בינארי. בהמשך רשומה זו נצטרך להשתמש בבסיס בינארי כדי לייצג את מצבי המעגל השונים. על ספירה בבסיס בינארי (ובכל בסיס אחר) כתבתי כבר בהרחבה בפוסט הזה.

שערים לוגיים

שערים לוגיים הם ייצוג אבסטרקטי של היחידות הלוגיות המרכיבות מעגלים דיגיטליים – בעזרתם נוכל להגדיר נסיבתיות במעגל, כלומר – דבר מסוים שקורה גורם לדבר אחר לקרות. ברשומה זו נשתמש בעיקר במהפכים ובשערי AND. להרחבה בנושא זה ניתן לקרוא את הפוסט הבא.

מעגלים משולבים

מעגלים משולבים (באנגלית Integrated Circuits או בקיצור IC) הם מה שאנחנו מכירים בתור "שבב", "צ'יפ" או "ג'וק". כל הרכיבים החשמליים שבהם התעסקנו עד כה הם רכיבים "פאסיביים", כאלה שאת התנהגותם ניתן לתאר על ידי משוואות בודדות ופשוטות. לעומת זאת המעגלים המשולבים הם רכיבים "אקטיביים", כאלה שבנויים בדרך כלל מטרנזיסטורים (מעין מתגים חשמליים קטנים) ויתפקדו בתור יחידות לוגיות שיכולות לבצע כל מיני פעולות מורכבות וספציפיות בתוך המעגל החשמלי.

בדרך כלל כשנרצה לשלב שער לוגי במעגל החשמלי שלנו, הוא יהיה ממומש בתור מעגל משולב (אם כי ישנן גם דרכים אחרות לממש שער לוגי, ונראה כאלה גם ברשומה זו). אך כמובן, מעגלים משולבים אינם מוגבלים לשימוש בתור שערים לוגיים בלבד, ויכולים להיות מימוש לחיישנים, מגברים, יחידות זיכרון, ועוד ועוד.

ישנן צורות שונות ומגוונות למעגלים המשולבים ("אריזות"), אך תמיד צורתן תהיה מרובעת ויהיו להם "רגליים" רבות שיתחברו לשאר המעגל החשמלי שלנו ויתפקדו בתור כניסות ויציאות של המעגל המשולב.

לכל מעגל משולב יהיו לפחות שתי רגליים שיקבלו את רמות המתח של המעגל השלם שלנו, בדרך כלל נקרא להן GND עבור הרמה הנמוכה ו-VDD עבור הרמה הגבוהה.

"הוראות ההפעלה" של המעגל המשולב הן מסמך datasheet שבו מפורט מה כל רגל של המעגל עושה, איך מפעילים אותו, באיזה מתחים הוא יכול לעבוד, באילו טמפרטורות, ועוד.

לדוגמה, זהו מסמך התיעוד של המעגל המשולב 74HC08. בתחילת המסמך מתואר כי זהו רכיב המכיל ארבעה שערי AND עצמאיים שאינם תלויים זה בזה, ושהרכיב נועד לפעול עם מתח עבודה בטווח של 2-6 וולט.

בנוסף, מצורף תרשים המקצה מספרים לכל אחת מהרגליים של הצ'יפ, ומתאר מה עושה כל רגל:

קל להבחין כי רגל מספר 7, הממוקמת בפינה התחתונה השמאלית של הצ'יפ, צריכה להתחבר לרמת המתח הנמוכה של המעגל, וכי רגל 14 בפינה הימנית העליונה מתחברת לרמת המתח הגבוהה של המעגל. עבור שאר הרגליים, המסמך מסביר כי הספרה מציינת את מספר השער והאות מסמנת את התפקיד. למשל, רגליים 1-2 הן הכניסות A,B של שער מספר 1, ורגל מספר 3 היא המוצא של השער. רגליים 12-13 הן הכניסות A,B של שער מספר 4, ורגל מספר 11 היא המוצא של אותו המהפך.

נושא שחשוב מאוד לשים לב אליו בנוגע למעגלים משולבים הוא התנגדות הכניסה.

עבור מעגלים משולבים רבים (וכל אלו שמופיעים ברשומה זו) התנגדות הכניסה היא אינסופית. המשמעות היא שלא זורם זרם חשמלי דרך הכניסות. בכלל.

הכניסות "רואות" את המתח החשמלי במעגל בנקודות אליהן הן מחוברות, אבל הזרם לא עובר דרכן כלל. המתחים שהכניסות "רואות" והלוגיקה הפנימית של המעגל המשולב ימתגו את היציאות של המעגל המשולב, ויקבעו עבור כל יציאה אם לקצר אותה אל רמת המתח הגבוהה או הנמוכה (כאמור, המעגל מחובר גם לכל אחת מרמות המתח).

בדרך כלל ההתנגדויות של יציאות המעגל המשולב לא יהיו אינסופיות – כלומר דרכן כן יכול לזרום זרם. עובדה זו יכולה לשמש אותנו לשני הכיוונים – גם כדי שיציאה שמחוברת לרמת המתח הגבוהה תוכל לספק מתח לרכיבים נוספים במעגל והזרם "יצא ממנה", וגם כדי שיציאה שמחוברת לרמת המתח הנמוכה תוכל להוות ניקוז אל "האדמה" עבור רכיבים אחרים במעגל והזרם החשמלי שעובר בהם "ייכנס אליה".

* ברשומה זו נזניח זמני השהייה על מנת לפשט את הניתוח החשמלי

הקובייה האלקטרונית של אפיק

הקדמה לקובייה של אפיק

נכון למועד כתיבת שורות אלו ניתן למצוא באתר האינטרנט של אפיק את כל הפרויקטים האפשריים ליצירה בחוג. בתור ילד הפרויקט שהכי הגניב אותי היה קוביית משחק אלקטרונית.

אמנם הלדים בתמונה עקומים, אך עדיין ניתן לראות בבירור שהם מרכיבים מעין צג שמכיל את מיקומי כל הנקודות שפאה כלשהי בקוביית משחק יכולה להכיל. בעזרת צירופים שונים של הלדים האלה ניתן להציג כל מספר אפשרי שמופיע בקוביית משחק רגילה.

כאשר לוחצים על הכפתור בפינה הימנית התחתונה של המעגל ומשאירים אותו לחוץ, הלדים נדלקים ונכבים כך שהמספרים 1-6 מתחלפים במהירות מסחררת על פני הצג. כאשר עוזבים את הכפתור הצג "נתקע" על המספר האחרון שהוצג בו. בגלל המהירות הגבוהה של התחלפות המספרים, לא ניתן לעצור את הצג על מספר רצוי, ולכן פעולה זו משולה להטלה של מספר אקראי בקובייה.

הדגמה חיה של הקוביה

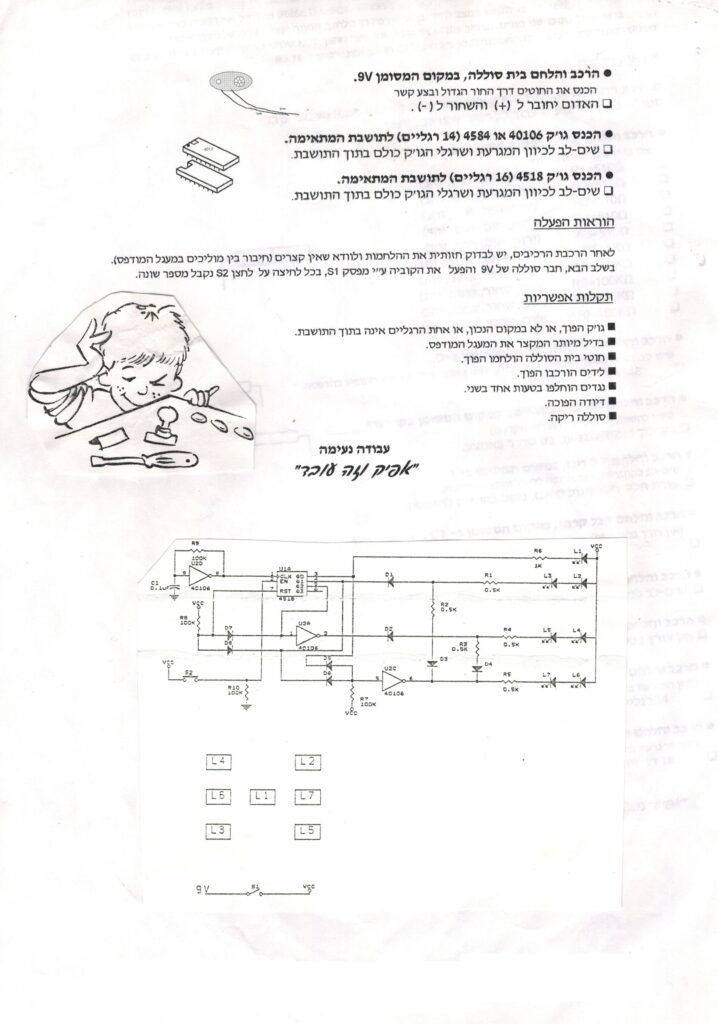
כדי להבין איך המעגל החשמלי הזה עובד, נצטרך קודם להבין מאילו רכיבים המעגל מורכב ומה כל אחד מהם עושה באופן כללי.

הרכיבים בקובייה של אפיק הם

מעגלים משולבים (צ'יפים):
- מהפך שמיט טריגר CD4584
- מונה בינארי CD4518
עשרה נגדים בהתנגדויות שונות
שמונה דיודות
שבע נורות LED
קבל לא מקוטב
כפתור

על רוב הרכיבים ברשימה הזו כבר דיברנו, אבל את שני הצ'יפים שמופיעים בה אנחנו עוד לא מכירים.

ובכן, נעים להכיר:

מהפך שמיט טריגר CD4584

נסתכל על הרכיב CD4584. מדובר בצ'יפ דיגיטלי המתנהג כמהפך עם שמיט טריגר.

כפי שכבר ראינו, מהפך הוא שער לוגי המקבל כניסה יחידה ומוציא פלט יחיד. עבור רמת מתח מסוימת בכניסה, המהפך יוציא את רמת המתח ההפוכה בפלט.

במעגל שלנו רמות המתח הן 9V ו-0V, לכן עבור מתח כניסה 9V יוציא המהפך 0V, ועבור מתח כניסה 0V המהפך יוציא 9V.

למרות רמות המתח המוגדרות היטב שלנו, העולם אינו שחור או לבן ולכן בפועל המתחים במעגל שלנו לא תמיד יהיו זהים בדיוק לרמות שהגדרנו. המתחים ינועו באופן רציף בכל הטווח שבין הרמות שהגדרנו. לכן מהפך רגיל יסתכל על נקודת האמצע בין רמות המתח, ויתייחס אל כל מתח שמתחתיה כ-0 לוגי ואל כל מתח שמעליה כאל 1 לוגי. כלומר, עבור רמות המתחים במעגל שלנו, ישתנה מתח היציאה של המהפך רק כאשר מתח הכניסה יחצה את רף ה-4.5V (מכל כיוון שהוא).

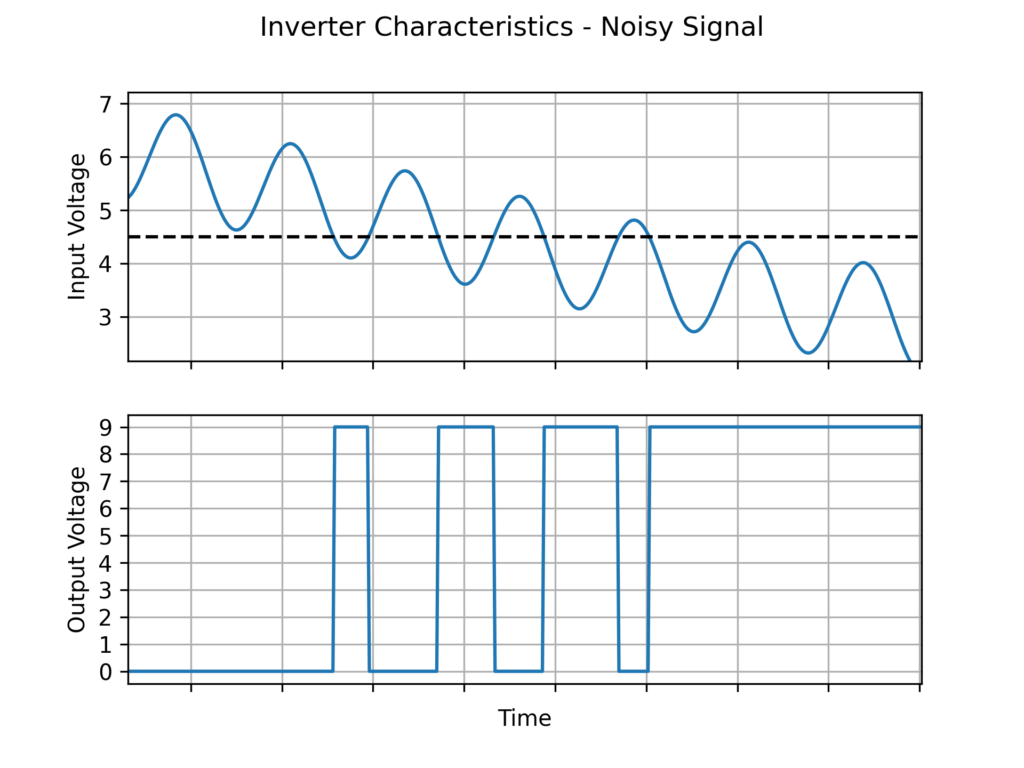
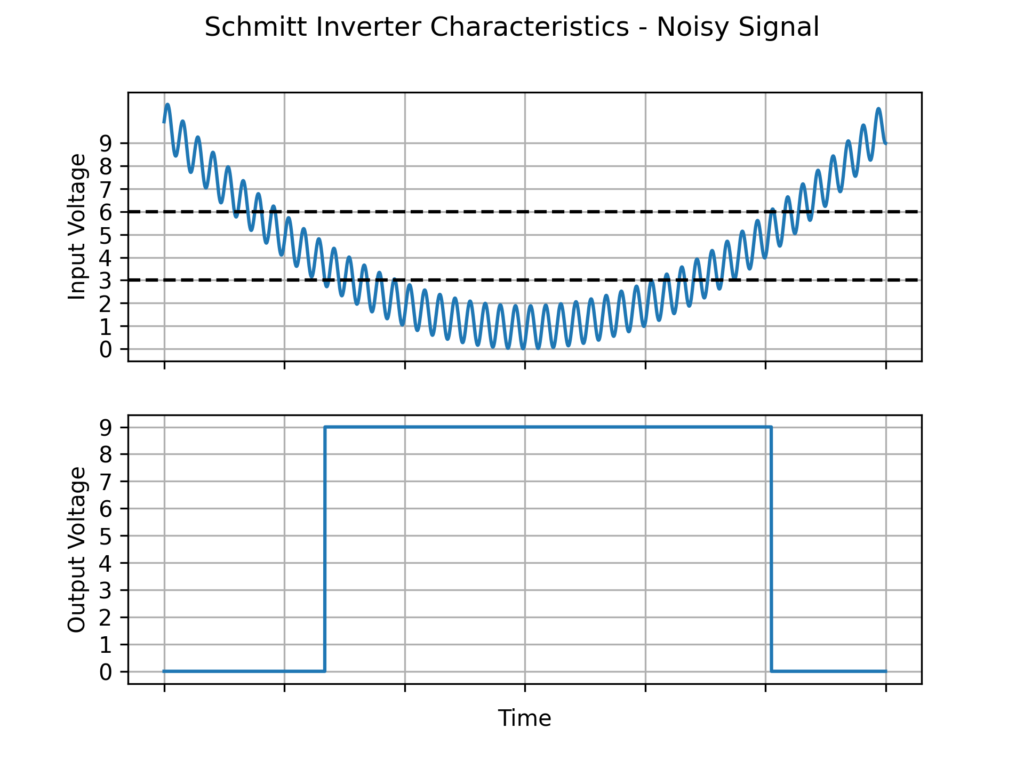
בדוגמה לעיל המהפך מבצע את תפקידו כראוי, אך במציאות האות החשמלי במעגל בדרך כלל לא יהיה יציב ו"חלק".

אופיין של מהפך עם אות כניסה פרבולי ורעש סינוסואידלי

בדוגמה הזאת אות הכניסה נשאר פרבולי אך מתווסף לו רעש בצורת גל סינוס. כתוצאה מכך המגמה העיקרית של הקלט נשארת זהה אך הוא מתנדנד סביב מתח הסף וחוצה אותו פעמים מרובות. כתוצאה מכך גם המוצא מתנדנד בין רמות המתח מספר פעמים לפני שהוא מתייצב על הרמה הנכונה.

אותה דוגמה, הפעם עם תקריב על נקודת העניין השמאלית

במקרים רבים זאת לא תהיה ההתנהגות שנרצה – נעדיף לקבל מעבר מוחלט ויציב בין רמות האנרגיה השונות מבלי לקבל "רעש" בפלט. על מנת להשיג את התנהגות זו משתמשים במהפך עם שמיט טריגר. המשמעות היא שבמקום מתח סף יחיד שיהפוך את המוצא כל פעם שמתח הכניסה יחצה אותו, יהיו לנו שני מתחי סף שונים והמוצא יתהפך רק כאשר מתח הכניסה יחצה את הסף שקרוב יותר למתח המוצא הנוכחי.

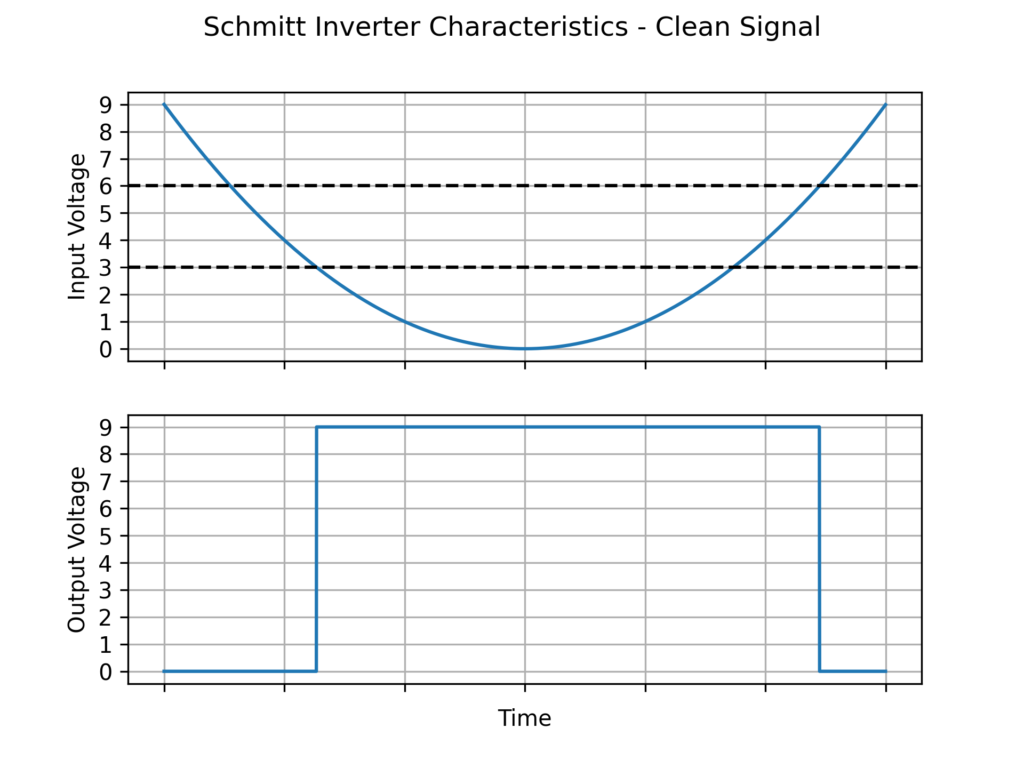
לדוגמה, עבור רמות האנרגיה 9V, 0V שקבענו, נבחר סף עליון 6V וסף תחתון 3V. כאשר מתח המוצא הוא 0, על מנת להפוך אותו ל-9V מתח הכניסה יצטרך לרדת אל מתחת לסף התחתון שלנו שהוא 3V. במצב ההפוך בו המוצא שלנו הוא 9V, על מנת להפוך אותו ל-0 מתח הכניסה יצטרך לעלות אל מעל 6V.

אופיין של מהפך שמיט טריגר עבור אות כניסה פרבולי

עבור אות כניסה פרבולי עם רעש סינוסואידלי, הפעם המהפך שמיט טריגר יתעלם מהתנודות ויפיק אות מוצא יציב ונקי:

אופיין של מהפך שמיט טריגר עם אות כניסה פרבולי ורעש סינוסואידלי

מונה בינארי CD4518

נסתכל על הרכיב C D 4518 ונראה שמדובר במעגל משולב המכיל שני מונים בינאריים בעלי 4 סיביות המופעלים בעליית השעון.

לכל אחד מהמונים יש שבעה פינים – מתוכם ארבעה הם יציאות המונה ונכנה אותם Q0-Q3 בהתאמה. שאר הפינים הם כניסות – יש לנו את כניסת ה-Clock, את כניסת ה-Enable ואת כניסת ה-Reset.

בתור התחלה נניח כי כניסת Enable מחוברת באופן קבוע לרמת המתח הגבוהה, כלומר Enable=1, וכי כניסת Reset מחוברת באופן קבוע לרמת המתח הנמוכה, כלומר Reset=0. נחזור לדבר עליהן אחר כך. במצב התחלתי זה, כל היציאות יוציאו רמת מתח נמוכה, כלומר Q0=Q1=Q2=Q3=0. כניסת ה-Clock חופשייה להשתנות, והיא משפיעה על היציאות שלנו: Q0-Q3 מייצגות מספר בינארי בן ארבע ספרות, כשהמספר הראשון הוא 0000. כל פעם שכניסת Clock משתנה מ-0 ל-1, המספר הבינארי שמייוצג על ידי Q0-Q3 ייגדל ב-1. נשים לב שכשאר Clock משתנה מ-1 ל-0 היציאות לא משתנות. לכן נאמר שהמונה מופעל בעליית השעון.

כאשר Q0=Q1=Q2=Q3=1 כלומר פלט המונה הוא 1111, בפעם הבאה שכניסת Clock תעלה מ-0 ל-1 היציאות ישתנו בחזרה למצב ההתחלתי Q0=Q1=Q2=Q3=0 כלומר לפלט 0000. המספר הבינארי 1111 בבסיס עשרוני שווה ל-15, כלומר הרכיב שלנו סופר מ-0 עד 15 וחוזר חלילה, כאשר בכל מחזור יש 16 מצבים (כולל 0).

את ההתנהגות הזאת אפשר לתאר בטבלה הבאה:

Decimal Number	Binary Number	Q0	Q1	Q2	Q3	Clock Tick	Enable
0	0000	0	0	0	0	0	1
1	0001	1	0	0	0	1	1
2	0010	0	1	0	0	2	1
3	0011	1	1	0	0	3	1
4	0100	0	0	1	0	4	1
5	0101	1	0	1	0	5	1
6	0110	0	1	1	0	6	1
7	0111	1	1	1	0	7	1
8	1000	0	0	0	1	8	1
9	1001	1	0	0	1	9	1
10	1010	0	1	0	1	10	1
11	1011	1	1	0	1	11	1
12	1100	0	0	1	1	12	1
13	1101	1	0	1	1	13	1
14	1110	0	1	1	1	14	1
15	1111	1	1	1	1	15	1
0	0000	0	0	0	0	16	1
1	0001	1	0	0	0	17	1
2	0010	0	1	0	0	18	1
3	0011	1	1	0	0	19	1
4	0100	0	0	1	0	20	1

וכן הלאה…

הנה עוד הדגמה לאורך זמן של רמות המתח משתנות במונה:

כעת נחזור לכניסות ה-Enable וה-Reset.

כניסת Enable קובעת האם המונה פעיל או לא. כל עוד Enable=1 כמו בדוגמה שתיארנו, המונה יתנהג כרגיל. לעומת זאת כאשר Enable=0, המונה לא יתקדם וישאר "תקוע" במצבו הנוכחי, ללא קשר לכניסת השעון. רק כאשר Enable יעלה בחזרה ל-1, המונה ימשיך להתקדם מהנקודה בה הוא נעצר.

כניסת Reset מאפשרת לאפס את המונה. כאשר Reset=0 המונה מתנהג כרגיל, אך כאשר Reset עולה ל-1 מוצא המונה יתאפס (Q0=Q1=Q2=Q3=0) וישאר במצב זה (ללא קשר לכניסות האחרות) עד ש-Reset יירד בחזרה ל-0. רק לאחר מכן המונה יחל להתקדם מחדש, החל ממצבו המאופס.

איך הקובייה של אפיק עובדת

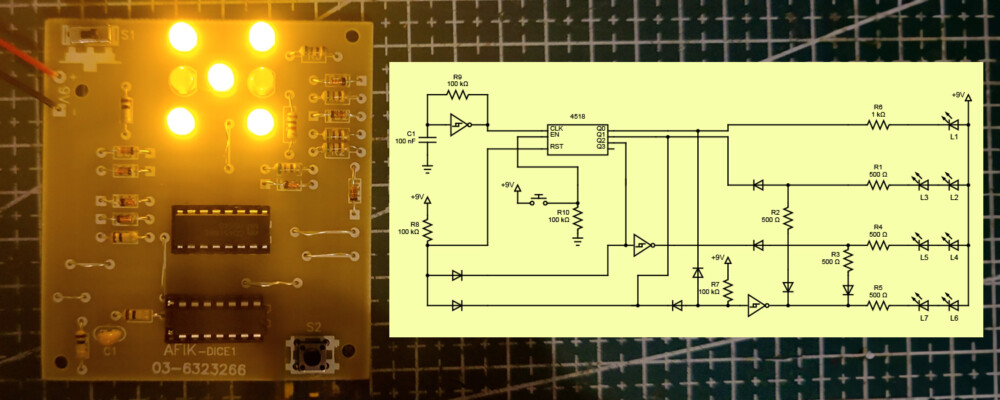
עכשיו כשאנחנו מכירים את הקונספטים והרכיבים הנדרשים, אפשר סוף סוף להסתכל על תרשים המעגל של הקובייה של אפיק:

(נשים לב שקיים חיבור בין קווים נחתכים רק כאשר קיימת נקודה מודגשת בחיתוך שלהם)

במבט שטחי המעגל הזה יכול להיראות מאיים – הרי מאיפה בכלל מתחילים לנסות לקרוא אותו? התשובה היא שמתחילים מהצ'יפ הכי מורכב – המונה 4518. כאשר מסתכלים על כל כניסה ויציאה שלו בנפרד, וזוכרים שהדיודות והמהפכים מעבירים זרם בכיוון יחיד בלבד, שמים לב שהמעגל הזה בעצם מחולק לארבעה תתי-מעגלים נפרדים, אשר כל אחד מהם מושפע מהמונה או משפיע עליו באופן שונה:

תת-המעגל הראשון שמתואר לעיל, מחובר לכניסת ה-Clock של המונה ובהמשך נראה כיצד הוא משפיע על קצב פעולת המונה.

תת-המעגל השני, אשר מחובר לכניסת ה-Enable של המונה וקובע מתי המונה מתקדם או מתי המונה מושהה.

תת-המעגל השלישי, אשר מחבר בין חלק מיציאות המונה לבין כניסת ה-Reset. מכאן ניתן להסיק שערכים מסוימים במוצא של המונה יגרמו לו להתאפס, ובהמשך נבין אילו.

תת-המעגל הרביעי, אשר מחבר בין מוצא המונה לבין נורות הלד. ערכים שונים במוצא המונה יגרמו לנורות שונות להידלק.

תת-מעגל ראשון – כניסת ה-Clock

נתחיל בהסתכלות על תת-המעגל הראשון:

כניסת ה-Clock של המונה מחוברת למוצא של המהפך-שמיט-טריגר שמסומן כ-U2D. נזכור שדרך כניסות של צ'יפים לא זורם זרם, לכן אפשר לחשוב עליהן כעל מד-מתח. במקרה שלנו המתח שכניסת ה-clock מגיבה אליו הוא מתח המוצא של המהפך. מוצא המהפך, בתורו, תלוי במתח הכניסה למהפך. נשים לב שכניסת המהפך ויציאתו מחוברות דרך נגד R9, כלומר קיים משוב במעגל.

כיוון שהמתח במוצא המהפך יכול להיות רק בשני מצבים (רמת מתח נמוכה או גבוהה), נפשט את המעגל ונחלק אותו לשני מצבים:

מצב ראשון (החלק העליון בתמונה) בו מוצא המהפך הוא 0 לוגי, ומצב שני (בתחתית התמונה) בו מוצא המהפך הוא 1 לוגי. כעת אפשר להסיר את המהפך משני המצבים. נסמן ב-Vc את המתח על הקבל C1.

במצב התחתון, הזרם במעגל זורם מהנקודה 9V דרך הנגד, ממנו אל הקבל וממנו אל האדמה. לכן במצב זה הקבל נטען.

במצב העליון, אין מקור מתח במעגל ושני קצוותיו מחוברים לאדמה. המטען שנאגר בקבל יעזוב אותו ויזרום דרך הנגד חזרה לאדמה. לכן במצב זה הקבל נפרק.

כיוון שהקבל נטען או נפרק, המטען עליו אינו קבוע – הוא משתנה בזמן. לכן במונחים מתמטיים, המטען בקבל הוא פונקציה שתלויה בזמן. אפשר לסמן אותה בתור $q(t)$ כאשר t הוא משתנה המייצג את הזמן.

במעגל שלנו הקבל מחובר בין כניסת המהפך לבין ההדק השלילי, כך שמתח הכניסה של המהפך הוא המתח על הקבל. בנוסף אנחנו יודעים שקיים קשר ישיר בין מטען האגור בקבל לבין המתח על אותו הקבל:

$V_{C}=\frac{q}{C}$

כאשר $q$ הוא המטען שצבור בקבל, $C$ הוא קיבול הקבל ו- $V_{C}$ הוא המתח על הקבל. כיוון ש-C קבוע בזמן ולא משתנה (במקרה שלנו $C=100\left [ nF \right ]$ ), המתח על הקבל גם הוא פונקציה שמקיימת את אותו הקשר לפונקציית המטען:

$V_{C}(t)=\frac{q(t)}{C}$ .

כל זה אומר שאם נדע איך נראית ומתנהגת פונקציית המתח על הקבל (שהיא מתח הכניסה למהפך), לפי האופיין של מהפך שמיט טריגר נוכל לדעת בדיוק איך תראה פונקציית המוצא של המהפך, שהיא גם כניסת ה-Clock של המונה.

כלומר, אם נמצא את פונקציית המתח על הקבל $V(t)$ , נדע איך מתנהגת כניסת ה-Clock של המונה – מידע הכרחי כדי להבין איך המונה מתנהג ומכך איך מתנהגת הקובייה של אפיק.

על מנת למצוא את $V(t)$ נצטרך לבצע ניתוח מתמטי למעגל:

* אלו שפחות מעוניינים לעקוב אחרי הפיתוח המתמטי מוזמנים לקפוץ ישר לתוצאה

ננתח כל אחד מהמצבים לחוד.

מצב 1 – פריקה

נניח שהמעגל מצוי במצב העליון – פריקה. בעזרת חוק המתחים של קירכהוף ננסח משוואה למציאת מתח הקבל: שני הרכיבים היחידים במעגל הם הקבל והנגד, ואין מקורות מתח. לכן סכום המתחים שלהם מתאפס:

(1) $\begin{equation*} V_{C}+V_{R}=0\end{equation*}$

כאשר $V_{R}$ הוא המתח על הנגד.

נזכור כי עבור נגדים מתקיים חוק אוהם:

(2) $\begin{equation*} V_{R}(t)=I(t)\cdot R\end{equation*}$

כאשר $I(t)$ היא פונקציית הזרם החשמלי שזורם בנגד בזמן t, ו- $R$ היא ההתנגדות הקבועה של הנגד (במקרה שלנו $R=100\left [ k\Omega \right ]$ ).

נוסף על כך, כפי שראינו קודם:

(3) $\begin{equation*} V_{C}(t)=\frac{q(t)}{C}\end{equation*}$

נציב את משוואה (2) ואת משוואה (3) אל תוך משוואה (1) ונקבל:

(4) $\begin{equation*} \frac{q(t)}{C}+I(t)\cdot R=0\end{equation*}$

בהגדרה, זרם חשמלי הוא תנועה של מטענים חשמליים. לכן הזרם החשמלי דרך הקבל הוא השינוי בזמן של המטען החשמלי על הקבל. הואיל והן הזרם והן המטען החשמליים הם פונקציות התלויות בזמן, השינוי בזמן של המטען הוא הנגזרת של פונקציית המטען לפי הזמן. ומכך, לפי הגדרת הזרם, הוכחנו שהזרם החשמלי הוא הנגזרת בזמן של המטען החשמלי.

בתיכון לימדו אותנו לייצג נגזרות לפי סימון לגראנז', כך שהנגזרת של הפונקציה $f(x)$ לפי x נכתבת בתור ${f}'(x)$

בחלק מבתי הספר מלמדים גם את סימון לייבניץ, שלפיו הנגזרת של $f(x)$ לפי x היא

$\frac{df}{dx}=\frac{df(x)}{dx}=\frac{d}{dx}f(x)$

אבל בדרך כלל כשהנגזרת היא ביחס לזמן, כמו במקרה שלנו, משתמשים בסימון ניוטון: $\dot{f}(x)$

ההבדל בסימונים הוא בעיקר סימבולי ופחות בעל השפעה מתמטית. אנחנו הולכים להשתמש בסימון ניוטון. אז:

(5) $\begin{equation*} I(t)=\frac{d}{dt}q(t)=\dot{q}(t)\end{equation*}$

נציב את זה במשוואה (4) ונקבל

$\frac{q(t)}{C}+\dot{q}(t)\cdot R=0$

ולאחר סידור קוסמטי קל (חלוקת כל המשוואה ב-R) נקבל

(6) $\begin{equation*} \boxed{\frac{q(t)}{RC}+\dot{q}(t)=0}\end{equation*}$

חשוב לשים לב שהמשוואה שקיבלנו כבר איננה משוואה אלגברית רגילה מהסוג שהתרגלנו לפתור בבית הספר – אם במשוואה "רגילה" הפתרון שאנחנו מחפשים הוא מספר אשר עבורו מתקיים השיוויון, במשוואה שאנחנו קיבלנו הפתרון שנחפש הוא פונקציה עבורה מתקיים השיוויון. למשוואה מסוג זה, בה אנו מחפשים פונקציה אשר מקיימת קשר מסוים עם הנגזרות של עצמה, קוראים משוואה דיפרנציאלית. ליתר דיוק, המשוואה שלנו היא משוואה דיפרנציאלית לינארית והומוגנית מסדר ראשון. הפונקציה שאנחנו מחפשים היא $q(t)$ שכזכור מתארת את המטען החשמלי בקבל ברגע נתון $t$ .

משוואות מסוג זה לא תמיד ניתן לפתור באופן אנליטי (כלומר לבצע פיתוח מתמטי שלב אחר שלב). למזלנו, מתמטיקאים טובים ונכונים כבר מצאו פתרונות לסוגים רבים של משוואות דיפרנציאליות. עבור משוואה מצורה זאת, הפתרון יהיה

(7) $\begin{equation*} q(t)=A\cdot e^{\alpha \cdot t}\end{equation*}$

כאשר $A$ ו- $\alpha$ הם פרמטרים שנצטרך למצוא על ידי התאמת הפתרון למעגל החשמלי הספציפי שלנו.

את $\alpha$ נוכל למצוא על ידי הצבת הפתרון שלנו במשוואה (6). בשביל לעשות את זה נצטרך לחשב קודם את הנגזרת $\dot{q}(t)$ על ידי כללי הגזירה:

(8) $\begin{equation*} \dot{q}(t)=\alpha\cdot A\cdot e^{\alpha \cdot t}\end{equation*}$

ועכשיו נציב את $\dot{q}(t)$ ואת $q(t)$ במשוואה (6) ונקבל

$\frac{1}{RC}\cdot \cancel{Ae^{\alpha \cdot t}}+\alpha\cdot \cancel{Ae^{\alpha \cdot t}}=0$

הביטוי $Ae^{\alpha \cdot t}$ מצטמצם ואנחנו נשארים עם

$\frac{1}{RC} + \alpha =0$

$\Downarrow$

$\boxed{\alpha =-\frac{1}{RC}}$

מצאנו את הערך של $\alpha$ ועכשיו אפשר להציב אותו בפתרון שלנו.

(9) $\begin{equation*} q(t)=A\cdot e^{-\frac{t}{RC}}\end{equation*}$

על ידי הצבת $q(t)$ במשוואה (3) נקבל את פונקציית המתח:

(10) $\begin{equation*} V_{C}(t)=\frac{A}{C}\cdot e^{-\frac{t}{RC}}\end{equation*}$

כעת פונקציית המתח על הקבל שלמה כמעט לחלוטין, נשאר למצוא רק את הפרמטר $A$ . ניזכר שאנחנו פותרים את המעגל עבור מצב פריקת הקבל. לכן נצפה כי בזמן $t=0$ הקבל יהיה טעון במלואו. כלומר:

$V_{C}(t=0)=9[V]$

נציב $t=0$ במשוואה (10), נשווה ל-9 ונקבל:

$\frac{A}{C}\cdot e^{-\frac{0}{RC}}=\frac{A}{C}\cdot e^{0}=\frac{A}{C}\cdot 1=\frac{A}{C}$

$\Downarrow$

$\frac{A}{C}=9$

$\Downarrow$

$A=9C$

מצאנו את הערך של $A$ ! נציב אותו בחזרה למשוואה (10) ונגיע לארץ המובטחת – משוואת המתח על הקבל בעת פריקה:

(11) $\begin{equation*} \boxed{V_{C}(t)=9e^{-\frac{t}{RC}}}\end{equation*}$

כשכמובן לפי הנתונים שלנו,

$R=100\left [ k\Omega \right ]$

$C=100[nF]$

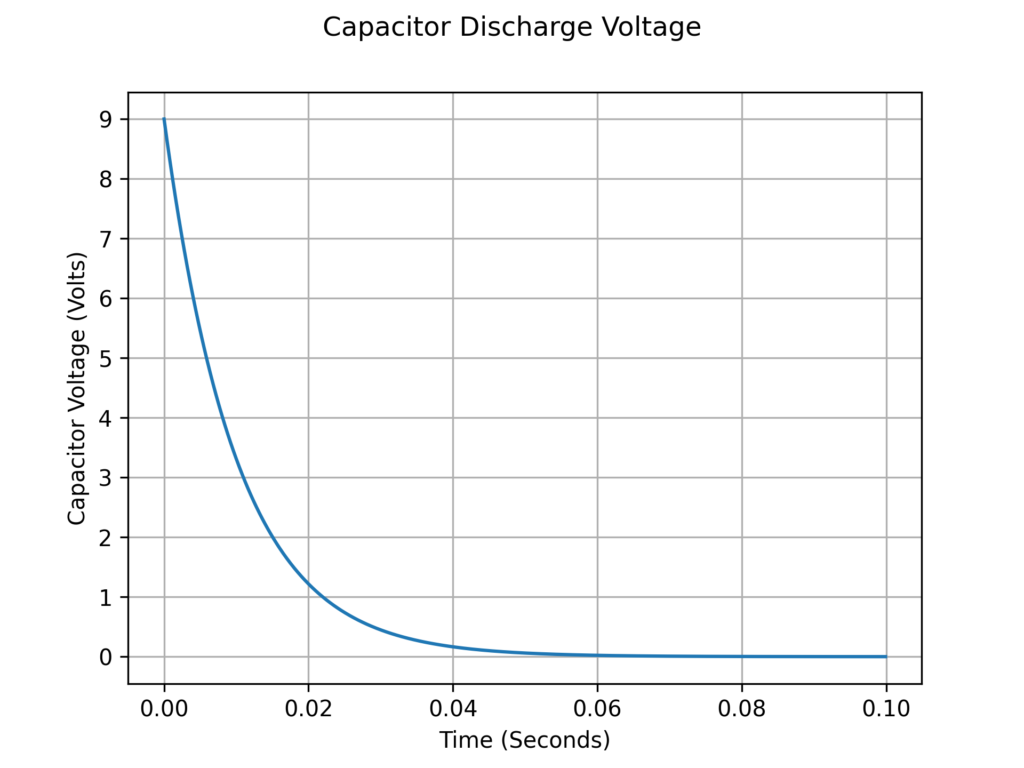
ככה זה נראה לאורך זמן:

הקבל נפרק בדעיכה אקספוננציאלית – כלומר ככל שהזמן עובר, קטן הקצב שבו המתח על הקבל נפרק, עד שהמתח מתייצב על 0. נשים לב שהקבל נפרק לחלוטין תוך פחות מעשירית השנייה. בקנה מידה של ראייה אנושית זה מאוד מאוד מהיר – יותר מהיר מלמצמץ.

מצב 2 – טעינה

נניח שהמעגל מצוי במצב התחתון – טעינה. ננסח שוב משוואת מתחים בעזרת חוק המתחים של קירכהוף: שני הרכיבים במעגל מחוברים בטור אל מקור מתח ברמת המתח הגבוהה שלנו (9V). לכן סכום המתחים שלהם הוא 9:

(12) $\begin{equation*} V_{C}+V_{R}=9\end{equation*}$

נפתח בדיוק לפי אותם השיקולים שביצענו עבור משוואה (6) ונקבל:

$\frac{q(t)}{C}+ \dot{q}(t) \cdot R =9$

$\Downarrow$

(13) $\begin{equation*} \frac{q(t)}{RC}+\dot{q}(t)=\frac{9}{R}\end{equation*}$

זוהי משוואה דיפרנציאלית לינארית שאינה הומוגנית מסדר ראשון. גם עבורה מתמטיקאים יפים ונכונים מצאו צורה כללית לפתרון:

(14) $\begin{equation*} q(t)=\underset{y_{P}(t)}{\underbrace{B\cdot e^{\beta \cdot t}}}+D\end{equation*}$

כאשר הדרישה היא ש- $y_{P}$ תפתור את הגרסה ההומוגנית של המשוואה, כלומר

$\frac{y_{P}(t)}{RC}+\dot{y_{P}}(t)=0$

שזה בדיוק מה שעשינו במצב הפריקה, כלומר

$\frac{1}{RC}\cdot \cancel{Be^{\beta\cdot t}}+\beta\cdot \cancel{Be^{\beta \cdot t}}=0$

$\Downarrow$

$\beta =-\frac{1}{RC}$

ולכן כשמציבים את הערך של $\beta$ לתוך משוואה (14) נשארים עם

(15) $\begin{equation*} q(t)=B\cdot e^{-\frac{t}{RC}}+D\end{equation*}$

$\dot{q}(t)=-\frac{B}{RC}\cdot e^{-\frac{t}{RC}}$

על מנת למצוא את $D$ נציב את משוואה (15) לתוך משוואה (13):

$\cancel{\frac{B\cdot e^{-\frac{t}{RC}}}{RC}}\cancel{-\frac{B \cdot e^{-\frac{t}{RC}}}{RC}}+\frac{D}{RC} = \frac{9}{R}$

$\Downarrow$

$\frac{D}{\cancel{R}C} = \frac{9}{\cancel{R}}$

$\Downarrow$

$D=9C$

ונציב את $D$ בחזרה לתוך משוואה (15)

(16) $\begin{equation*} q(t)=B\cdot e^{-\frac{t}{RC}}+9C\end{equation*}$

וגם הפעם נציב במשוואה (3) כדי לקבל את פונקציית המתח:

(17) $\begin{equation*} V_{C}(t)=\frac{B\cdot e^{-\frac{t}{RC}}+9C}{C}\end{equation*}$

כעת פונקציית המתח על הקבל שלמה כמעט לחלוטין, נשאר למצוא רק את הפרמטר $B$ . הפעם, בגלל שאנחנו במצב טעינה, נדרוש כי בזמן $t=0$ המתח על הקבל יהיה אפס (כי הוא עדיין לא הספיק להיטען). נציב $t=0$ בפונקציית המתח ונשווה לאפס.

$\frac{B\cdot e^{-\frac{0}{RC}}+9C}{C}=\frac{B\cdot e^{0}+9C}{C}=\frac{B\cdot 1+9C}{C}=\frac{B+9C}{C}=0$

$\Downarrow$

$B=-9C$

נציב בפונקציית המתח את הערך של $B$ ונישאר עם

$V_{C}(t)=\frac{-9C\cdot e^{-\frac{t}{RC}}+9C}{C}=9\frac{(1-e^{-\frac{t}{RC}})\cancel{C}}{\cancel{C}}$

$\Downarrow$

(18) $\begin{equation*} \boxed{V_{C}(t)=9(1- e^{-\frac{t}{RC}})}\end{equation*}$

ובשעה טובה הגענו שוב פעם לביטוי הסופי. כך הוא נראה לאורך זמן:

הפעם הקבל נטען במגמה אספוננציאלית, כך שככל שהזמן עובר קצב הטעינה של הקבל יורד, עד שהוא מתייצב על המתח המקסימלי – רמת המת הגבוה שלנו. גם במקרה הזה, הקבל נטען בשלמותו תוך פחות מעשירית השנייה. מהיר וכל זה.

ניזכר כי מוצא המהפך שמיט טריגר עולה מ-0 לוגי ל-1 לוגי כאשר המתח על הקבל יורד מתחת ל-3V. בנוסף, מוצא המהפך יורד מ-1 לוגי ל-0 לוגי כאשר המתח על הקבל עולה מעל ל-6V.

אז תוצאת הניתוח המתמטי שלנו היא:

כאשר בתהליך הטעינה המתח על הקבל עולה מעל רף ה-6V, מוצא המהפך יורד מ-9V ל0V כך שתהליך הטעינה נפסק מיידית ואנחנו נכנסים לתהליך הפריקה. כאשר המתח על הקבל יורדת מתחת לרף ה-3V, מוצא המהפך עולה בחזרה מ-0V ל-9V ובכך תהליך הפריקה נפסק מיידית ואנחנו חוזרים לתהליך הטעינה. וחוזר חלילה.

שני המצבים הללו ממתגים זה את זה, תקועים בלולאה אינסופית של טעינה ופריקה. כיוון שמתח הכניסה של ה-Clock במונה הבינארי זהה למתח המוצא של המהפך, הסיגנל שהמונה הבינארי מקבל הוא גל ריבועי שקופץ במחזוריות בין רמת מתח גבוהה לרמת מתח נמוכה.

בשפה המקצועית, תת המעגל הזה נקרא אוסילטור.

מכך, לפי התפקיד של כניסת ה-Clock במונה הבינארי, כל פעם שמתח השעון עולה מ-0 לוגי ל-1 לוגי, המספר במוצא המונה הבינארי גדל ב-1. זוהי מטרתו של תת-המעגל הראשון – להיות המנוע של המונה, ולקדם את הספירה. לולא האוסילטור, המונה היה נשאר קפוא בזמן לנצח.

מהגרף קל לקרוא כי הזמן שעובר בין עלייה של השעון לבין העלייה הבאה (זמן המחזור), הוא כ-14 מילי-שניות.

$T=14\cdot 10^{-3}[ms]$

כלומר כל מספר מוצג על ידי המונה במשך 14 מילי-שניות בלבד. או לחילופין, לפי הקשר בין זמן מחזור לתדירות

$f= \frac{1}{T}$

תדר השעון של המונה הוא בערך 71 הרץ, כלומר בכל שנייה המונה מספיק להתקדם 71 פעמים בין המספרים.

* חישוב אנליטי ומעמיק יותר של תדר האוסילטור אפשר לקרוא כאן

עכשיו כשהבנו את המשמעות והתפקיד של תת-המעגל הראשון (שהוא גם המסובך ביותר להבנה), אפשר להתקדם אל תת-המעגל הבא. מכאן והלאה תתי-המעגל יהיו פשוטים בהרבה.

תת-מעגל שני – כניסת ה-Enable

נתמקד בתת-המעגל השני.

תת-מעגל זה שולט בכניסת ה-Enable. כזכור, כניסה זו שולטת גם היא בקידום המספרים במונה. כל עוד Enable=0 לוגית, המונה מתעלם לחלוטין מכניסת ה-Clock וישאר קפוא על המספר האחרון שהוצג בו. רק כאשר Enable=1 לוגית, המונה מתייחס לכניסת השעון ומתקדם בספירה בהתאם אליה.

במקרה שלנו, Enable מחוברת במקביל לשני ענפים שונים במעגל:

ענף מתחבר אל הנגד R10 וממנו מתנקז אל ההדק השלילי במעגל
ענף המתחבר לכפתור. מצידו השני הכפתור מקבל אספקת 9V.

תפקוד המעגל תלוי במצב הכפתור – האם הוא לחוץ או לא לחוץ.

כאשר הכפתור במנוחה, Enable מחוברת לנגד R10 וממנו אל ההדק המעגל השלילי. כפי שאנחנו יודעים לגבי כניסות במעגלים משולבים, דרך Enable לא זורם זרם. לכן לנגד R10 אין משמעות – אם אין זרם המתח שנופל עליו מתאפס. לכן המתח ש-Enable "רואה" הוא המתח בהדק השלילי של המעגל, כלומר 0V.

אז כפתור במנוחה גורר Enable=0.

כאשר הכפתור לחוץ, מתח העבודה 9V מחובר ישירות לנגד R10 וממנו ממשיך אל ההדק השלילי. כלומר זורם זרם. במעגל זה נגד R10 הוא הרכיב היחידי ולכן כל המתח נופל עליו. במקרה זה Enable "רואה" את המתח לפני שהוא נופל על הנגד, כלומר את המתח במלואו.

מכאן כפתור לחוץ גורר Enable=1.

תת-מעגל זה מכונה בשפה המקצועית "Pull-Down Resistor" (לצערי אני לא מצליח למצוא את החלופה העברית לביטוי) ומטרתו "למשוך מטה" את מתח המוצא כאשר הכפתור אינו לחוץ: במקרה בו נגד R10 לא היה קיים ו-Enable הייתה מחוברת ישירות לכפתור, כאשר הכפתור אינו לחוץ Enable למעשה "תלויה באוויר". כלומר לא מחוברת לכלום, מה שמכונה לפעמים hi-Z. אנחנו לא יכולים להניח כלום על מצב כזה – כאשר Enable תלויה באוויר היא לא מחוברת לא ל-0 לוגי ולא ל-1 לוגי, וזהו חוסר ודאות שאנחנו לא מעוניינים בו. בדיוק את הבעיה הזאת פותר Pull-Down Resistor על ידי משיכת Enable ל-0 לוגי כאשר הכפתור אינו לחוץ.

קונפיגורציה הפוכה לזאת נקראת "Pull-Up Resistor" ובה כאשר הכפתור אינו לחוץ המוצא "נמשך מעלה" אל 1 לוגי, וכאשר הוא לחוץ המוצא "נמשך מטה" כלפי 0 לוגי. כלומר תפקוד הכפתור התהפך. על Pull-Up Resistor ועל Pull-Down Resistor ניתן לקרוא בהרחבה כאן או במאמר הקצר הזה.

אז לפי תפקידה של כניסת Enable והמצבים שהסקנו מנגד ה-Pull-Down, המונה הבינארי יהיה מושהה כל עוד הכפתור אינו לחוץ. רק כאשר הכפתור לחוץ, המונה יתקדם בספירתו על ידי האוסילטור שמחובר בכניסת ה-Clock. זהו בדיוק השימוש הרצוי לכפתור:

כאשר הכפתור לחוץ הקובייה עוברת במהירות בין מספרים ומצויה באי ודאות, מצב זה שקול לשקשוק קובייה פיזית בכף היד. כאשר עוזבים את הכפתור הקובייה נעצרת על המספר האחרון שהוצג בה, מצב זה שקול להתייצבות הקוביה על משטח כאשר המספר הנבחר מופיע בפאתה העליונה.

תת-מעגל שלישי – כניסת ה-Reset

נתמקד בתת-המעגל השלישי.

בתת-מעגל זה, מתח העבודה 9V שלנו מחובר אל נגד R8, כאשר הדקו השני של הנגד מסתעף אל שלושה ענפים:

כניסת ה-Reset של המונה
יציאת Q2 של המונה דרך דיודה D7
יציאת Q1 של המונה דרך דיודה D8

נזכור כי כל עוד Reset=0 המונה מתנהג כרגיל, אך כאשר Reset=1 מוצא המונה מתאפס לחלוטין (Q0=Q1=Q2=Q3=0) ונשאר במצב זה עד ש-Reset יחזור ל-0. כלומר – על מנת להבין כיצד תת-מעגל זה משפיע על התנהגות המונה, נדרש לבדוק מה יהיה הערך של Reset עבור כל קומבינציה של Q1 ו-Q2.

Q1=0, Q2=0

במצב זה Q1 ו-Q2 שוות 0 לוגי. לכן הזרם זורם מנקודת ה-9V דרך נגד R8 ודרך שני הענפים אל האדמה. בהנחה שהדיודות במעגל קרובות להיות אידיאליות, ניתן להזניח את המתח שנופל עליהן. לכן נגד R8 הוא הרכיב היחידי במעגל ועליו נופל מלוא המתח. כלומר המתח לאחר הנגד הוא 0, וזה גם המתח שכניסת ה-Reset "רואה".

לכן במצב זה Reset=0 לוגית.

Q1=0, Q2=1

במצב זה Q1 שווה 0 לוגי ו-Q2 שווה 1 לוגי. כזכור זרם חשמלי זורם ממתח גבוה למתח נמוך. המתח המעשי ב-Q2 הוא 9V, אך אינו יכול לזרום אל האדמה ב-Q1 מפני שכיוון זה הפוך לכיוון הדיודה D7. לכן לא זורם זרם כלל דרך הענף של D7. מכך, הזרם זורם מנקודת ה-9V דרך נגד R8 ודרך הדיודה D8 בלבד אל האדמה. נגד R8 הוא הרכיב היחידי במעגל ועליו נופל מלוא המתח. כלומר המתח לאחר הנגד הוא 0, וזה גם המתח שכניסת ה-Reset "רואה".

מכאן, גם במצב זה Reset=0 לוגית.

Q1=1, Q2=0

במצב זה Q1 שווה 1 לוגי ו-Q2 שווה 0 לוגי. הניתוח זהה למצב הקודם, רק שהפעם דרך D7 זורם הזרם, ודרך D8 לא זורם זרם.

מכאן, גם במצב זה Reset=0 לוגית.

Q1=1, Q2=1

הפעם Q1 וגם Q2 שוות 1 לוגי. במצב זה כל המתחים המעשיים במעגל הם 9V – אין הפרשי מתחים ולכן לא זורם זרם חשמלי כלל. כיוון שאין זרם דרך נגד R8, גם לא נופל עליו מתח. כלומר Reset "רואה" 9V.

במצב זה Reset=1 לוגית.

נסכם את כל המצבים לכדי טבלה:

מצב	Q1	Q2	Reset
ראשון	0	0	0
שני	0	1	0
שלישי	1	0	0
רביעי	1	1	1

קיבלנו מעגל שבו Reset=1 אך ורק כאשר גם Q1 וגם Q2 שווים 1. בכל מצב אחר, Reset=0. בדיוק כמו במקרה של שער AND. ואכן, זהו מימוש של שער AND בלוגיקת דיודות.

בהקשר של הקוביה, תת-מעגל 3 יגרום לכך שהמונה יתאפס בפעם הראשונה שבה Q1 ו-Q2 יהיו בו זמנית ברמת מתח גבוהה. זה יקרה כאשר המונה יציג את המספר הבינארי 0110. בבסיס עשרוני המספר הזה הוא 6. כלומר, המונה שלנו סופר מ-0 עד 5, מכיוון שברגע שהוא מגיע ל-6 הוא מתאפס מיידית.

באופן הזה תת-מעגל 3 כופה על המונה לעבור בין שישה מצבים שונים (כולל אפס) וחוזר חלילה, במקום לעבור בין 16 מצבים שונים שהמונה מאפשר למנות. במילים אחרות, התפקיד של תת-מעגל 3 הוא להתאים את מספר המצבים שהמונה עובר ביניהם אל מספר הפאות שקיימות בקוביית משחק רגילה.

תת-מעגל רביעי – תצוגת הקובייה

נתמקד בתת-המעגל הרביעי, שבו סוף-סוף משתתפים הלדים שיציגו את פלט הקובייה. בסכימת המעגל, הלדים הם הדיודות L1-L7 כאשר החצים שיוצאים מהן מסמנים את האור הנפלט מהלד (אחרי הכל לדים הם דיודות פולטות אור). סידור הלדים על גבי הלוח הפיזי נראה כך:

ובעזרת הלדים הללו ניתן לייצג את הספרות 1-6:

מהתבוננות שטחית במעגל, נשים לב ששבעת הלדים מפוזרים על פני ארבעה ענפים בלבד, וכי חלק מהלדים מחוברים בטור אחד אחר השני. כלומר – לדים המחוברים בטור כחלק מאותו הענף, בהכרח יאירו ביחד. נמספר את הענפים הללו מ-A עד D מהענף העליון ביותר עד לתחתון ביותר, כדלהלן:

החלוקה הזו לענפים מאוד יעילה עבור ייצוג המספרים 1-6, שכן ניתן ליצור כל אחד מהם על ידי קומבינציה של הענפים A-D:

על ידי הדלקת ענף A בלבד
על ידי הדלקת ענף B בלבד
על ידי הדלקת הענפים A+B סימולטנית
על ידי הדלקת הענפים B+C סימולטנית
על ידי הדלקת הענפים A+B+C סימולטנית
על ידי הדלקת הענפים B+C+D סימולטנית

כעת נחזור לתת-המעגל הרביעי. נשים לב שכשמתחשבים בסידור הדיודות ניתן לפצל את תת-מעגל זה לשני תתי-תתי מעגל (🥴) נוספים:

תת-מעגל 4.1

תת-מעגל 4.2

נתמקד קודם בתת-מעגל 4.1:

הזרם מתחיל בנקודת ה-9V, משם מתפצל לשלושת הענפים A, B, C כאשר A העליון ביותר ו-C התחתון. כל ענף מסתיים באחת מיציאות המונה Q0-Q2.

על מנת שיזרום זרם בענף כלשהו, צריך להתקיים הפרש מתחים בין הנקודה 9V לבין קצה הענף. כלומר, עבור ענפים A,B זה יקרה אך ורק כאשר יציאת המונה המתאימה שווה 0 לוגית. בענף C המצב שונה מעט בעקבות המהפך U2A שמחובר בין דיודה D2 למוצא המונה Q2. הרכיב U2A חוצץ בין צידי הענף, לכן מה שמעניין אותנו הוא שמוצא המהפך יהיה 0 לוגי, וזה יקרה רק כאשר Q2=1 לוגית.

נסכם:

ענף A המכיל את לד L1 יופעל רק כאשר Q0=0
ענף B המכיל את הלדים L2,L3 יופעל רק כאשר Q1=0
ענף C המכיל את הלדים L4,L5 יופעל רק כאשר Q2=1

כעת ניתן להסתכל על כל אחד ממצבי המונה ולשבץ אילו מהענפים ידלקו בו:

Decimal Number	Binary Number	Q0	Q1	Q2	ענף A	ענף B	ענף C
0	0000	0	0	0	✅	✅	❌
1	0001	1	0	0	❌	✅	❌
2	0010	0	1	0	✅	❌	❌
3	0011	1	1	0	❌	❌	❌
4	0100	0	0	1	✅	✅	✅
5	0101	1	0	1	❌	✅	✅

בינתיים במצב 3 בטבלה כל הלדים כבויים, אך זאת אינה התמונה המלאה. על מנת להבין אותה צריך להסתכל גם על

תת-מעגל 4.2:

ראשית נבחין כי ענף A לא משתתף בתת-מעגל זה. הענף הכי עליון בשרטוט הוא ענף B.

שנית, נבחין כי כל הענפים שכן משתפפים בתת-מעגל זה (B,C,D) מתחברים לאותה נקודה – מוצא המהפך U2C (שהוא לא המהפך U2A מתת-המעגל הקודם). כלומר כאשר מוצא U2C יהיה 0 לוגי, הענפים B,C,D כלומר כל הלדים במעגל מלבד L1, ידלקו ביחד. על מנת שמוצא U2C יהיה 0 לוגי, כניסת U2C צריכה להיות 1 לוגי.

נשים לב שהמעגל שמחובר לכניסתו של U2C זהה לגמרי לתצורה של תת-מעגל 3 – כלומר הכניסה של U2C תהיה 1 לוגי אך ורק כאשר Q0=Q1=1 לוגית.

אז נסכם: כאשר Q0=Q1=1 לוגית, נדלקים בו זמנית ענפים B,C,D. כיוון שהמונה סופר רק מ-0 עד 5, המצב היחיד שבו זה יקרה יהיה כאשר המונה ימנה 3, בבינארית זה 0011. זה גם בדיוק המצב שהיה חסר לנו בטבלה. נוסיף אותו לשם:

Decimal Number	Binary Number	ענף A	ענף B	ענף C	ענף D
0	0000	✅	✅	❌	❌
1	0001	❌	✅	❌	❌
2	0010	✅	❌	❌	❌
3	0011	❌	✅	✅	✅
4	0100	✅	✅	✅	❌
5	0101	❌	✅	✅	❌

נתרגם את הטבלה לפי ניתוח הקומבינציות שביצענו קודם לכן:

במצב 0 פועלים ענפים A,B יחדיו. A+B=3
במצב 1 פועל ענף B לבדו. B=2
במצב 2 פועל ענף A לבדו. A=1
במצב 3 פועלים ענפים B,C,D יחדיו. B+C+D=6
במצב 4 פועלים ענפים A,B,C יחדיו. A+B+C=5
במצב 5 פועלים ענפים B,C יחדיו. B+C=4

לכן טבלת המצבים הסופית של הקוביה תראה כך:

Decimal Number	Binary Number	תצוגה
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101

בסרטון הבא אפשר לראות הדגמה של הקוביה בהילוך איטי, ולהיווכח שזהו אכן סדר המצבים בקובייה:

ובעצם, כאן סיימנו.

את כל הניתוח של הקובייה של אפיק.

סיכום

הקובייה של אפיק היא מעגל מודפס המכיל מערך של 7 לדים – אלו נועדו להציג את פאות הקובייה. למעגל מחובר כפתור, כאשר לוחצים עליו מערך הלדים מציג מהר מאוד בלולאה את כל פאות הקובייה, וכאשר משחררים את הכפתור התצוגה נעצרת על פאה מסוימת שנבחרה אקראית.

מבחינה לוגית, במרכז סכימת המעגל מצוי מונה בינארי המחובר לארבעה תתי מעגלים: הראשון הוא אוסילטור שמפעיל את שעון המונה, השני מנהל את הקלט מהכפתור. תת המעגל השלישי דואג לאפס את המונה מוקדם מספיק כדי שהלולאה שלו תכיל רק שישה מצבים, ותת המעגל הרביעי דואג להדליק את הלדים המתאימים לכל אחד ממצבי המונה.

המושגים, הרעיונות והטכניקות שהוצגו ברשומה זו הינם כלים משמעותיים להבנה של כל מעגל אלקטרוני אחר, ולמעשה כלים אלו מספיקים כדי להבין את הרוב המוחלט של הפרויקטים האחרים מחוג האלקטרוניקה של אפיק.

אם מתחשק לכם לבנות קוביית-אפיק בעצמכם, נכון למועד כתיבת שורות אלו עדיין ניתן להזמין את הערכה ישירות מהאתר של אפיק טכנולוגיות. אפשרות נוספת היא להשתמש בגרסה המחודשת לקובייה, שיצרתי בעצמי לצורך כתיבת רשומה זו (סכימת המעגל זהה, בעיקר שינויים קוסמטיים בעיצוב הפיזי. אפיק אם אתם קוראים את זה בבקשה אל תתבעו אותי).

ניתן להזמין את המעגל המודפס ישירות מכאן, או להוריד את קבצי הפרויקט שלו (gerbers) מכאן ולשלוח לכל שירות של ייצור PCB שמתאים לכם.

פוסטים לפי קטגוריה

הרשמה לעדכונים במייל

הקובייה האלקטרונית של אפיק

בכיתה ג' הייתי בחוג אלקטרוניקה

מבוא למעגלים חשמליים

מבוא לאלקטרוניקה דיגיטלית

מה זה אומר בכלל אלקטרוניקה דיגיטלית?

בסיס בינארי

שערים לוגיים

מעגלים משולבים

הקובייה האלקטרונית של אפיק

הקדמה לקובייה של אפיק

הרכיבים בקובייה של אפיק הם

מהפך שמיט טריגר CD4584

מונה בינארי CD4518

איך הקובייה של אפיק עובדת

תת-מעגל ראשון – כניסת ה-Clock

מצב 1 – פריקה

מצב 2 – טעינה

תת-מעגל שני – כניסת ה-Enable

תת-מעגל שלישי – כניסת ה-Reset

Q1=0, Q2=0

Q1=0, Q2=1

Q1=1, Q2=0

Q1=1, Q2=1

תת-מעגל רביעי – תצוגת הקובייה

נתמקד קודם בתת-מעגל 4.1:

תת-מעגל 4.2:

סיכום

רשומות נוספות בבלוג:

נכתבה תגובה אחת לרשומה זאת

כתיבת תגובה

פוסטים לפי קטגוריה

פוסטים לפי קטגוריה

נושאים פופולאריים

הרשמה לעדכונים במייל

הקובייה האלקטרונית של אפיק

בכיתה ג' הייתי בחוג אלקטרוניקה

מבוא למעגלים חשמליים

מבוא לאלקטרוניקה דיגיטלית

מה זה אומר בכלל אלקטרוניקה דיגיטלית?

בסיס בינארי

שערים לוגיים

מעגלים משולבים

הקובייה האלקטרונית של אפיק

הקדמה לקובייה של אפיק

הרכיבים בקובייה של אפיק הם

מהפך שמיט טריגר CD4584

מונה בינארי CD4518

איך הקובייה של אפיק עובדת

תת-מעגל ראשון – כניסת ה-Clock

מצב 1 – פריקה

מצב 2 – טעינה

תת-מעגל שני – כניסת ה-Enable

תת-מעגל שלישי – כניסת ה-Reset

Q1=0, Q2=0

Q1=0, Q2=1

Q1=1, Q2=0

Q1=1, Q2=1

תת-מעגל רביעי – תצוגת הקובייה

נתמקד קודם בתת-מעגל 4.1:

תת-מעגל 4.2:

סיכום

רשומות נוספות בבלוג:

נכתבה תגובה אחת לרשומה זאת

כתיבת תגובה

פוסטים לפי קטגוריה

נושאים פופולאריים